문제
직선 위에 위치를 나타내는 0, 1, 2, ...와 같은 음수가 아닌 정수들이 일정한 간격으로 오른쪽 방향으로 놓여 있다. 이러한 위치들 중 N개의 위치에 하나씩 점들이 주어진다(<그림 1>). 주어진 점들의 위치는 모두 다르다. 두 점 사이의 거리는 두 점의 위치를 나타내는 수들의 차이이다. <그림 1>에서는 4개의 점이 주어지고 점 a와 b의 거리는 3이다.

<그림 1>
각 점은 N개의 색깔 중 하나를 가진다. 편의상, 색깔은 1부터 N까지의 수로 표시한다.
각 점 p에 대해서, p에서 시작하는 직선 화살표를 이용해서 다른 점 q에 연결하려고 한다. 여기서, 점 q는 p와 같은 색깔의 점들 중 p와 거리가 가장 가까운 점이어야 한다. 만약 가장 가까운 점이 두 개 이상이면 아무거나 하나를 선택한다.
모든 점에 대해서 같은 색깔을 가진 다른 점이 항상 존재한다. 따라서 각 점 p에서 시작하여 위 조건을 만족하는 q로 가는 하나의 화살표를 항상 그릴 수 있다.
예를 들어, 점들을 순서쌍 (위치, 색깔) 로 표시할 때, a = (0,1), b = (1, 2), c = (3, 1), d = (4, 2), e = (5, 1)라고 하자.
아래 <그림 2>에서 이 점들을 표시한다. 여기서 흰색은 1, 검은색은 2에 해당된다.

<그림 2>
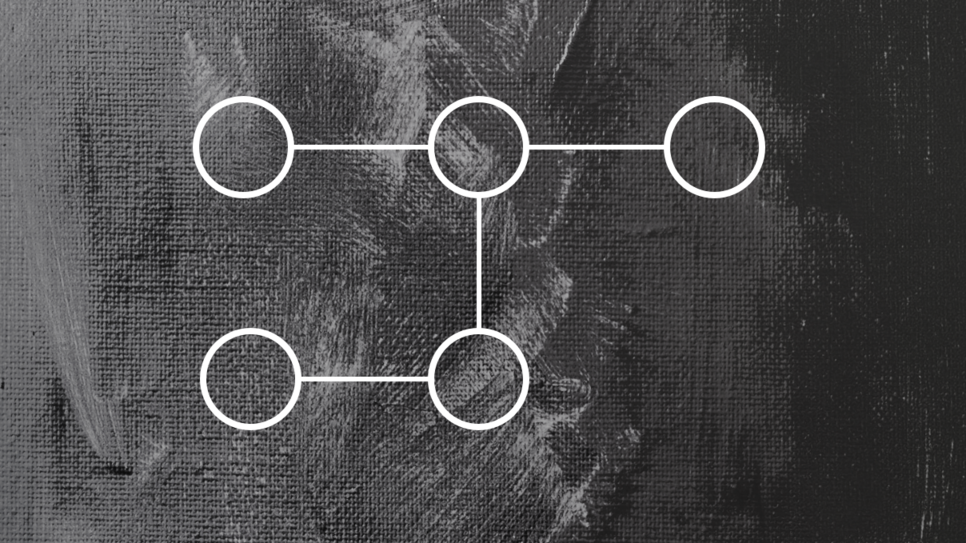
위의 조건으로 화살표를 그리면, 아래 <그림 3>과 같이 점 a의 화살표는 c로 연결된다. 점 b와 d의 화살표는 각각 d와 b로 연결된다. 또한 점 c와 e의 화살표는 각각 e와 c로 연결된다. 따라서 모든 화살표들의 길이 합은 3 + 3 + 2 + 3 + 2 = 13이다.

<그림 3>
점들의 위치와 색깔이 주어질 때, 모든 점에서 시작하는 화살표들의 길이 합을 출력하는 프로그램을 작성하시오.
입력
표준 입력으로 다음 정보가 주어진다. 첫 번째 줄에는 점들의 개수를 나타내는 정수 N이 주어 진다. 다음 N개의 줄 각각에는 점의 좌표와 색깔을 나타내는 두 정수 x와 y가 주어진다.
출력
표준 출력으로 모든 점에서 시작하는 화살표들의 길이 합을 출력한다.
제한
모든 서브태스크에서 점들의 위치 x와 색깔 y는 각각 0 ≤ x ≤ 105, 1 ≤ y ≤ N를 만족한다.
서브태스크 1 (25점)
점들이 가진 각 색깔 c에 대해서, 색깔 c를 가진 점은 정확히 두 개 존재하고 점들의 개수는 2 ≤ N ≤ 10를 만족한다.
서브태스크 2 (31점)
점들의 색깔은 모두 동일하고 점들의 개수는 2 ≤ N ≤ 300를 만족한다.
서브태스크 3 (33점)
점들의 색깔은 정확히 두 가지이고 점들의 개수는 2 ≤ N ≤ 1,000를 만족한다.
서브태스크 4 (11점)
점들의 개수는 2 ≤ N ≤ 5,000를 만족한다.

이문제의 핵심은 색깔별로 점들을 봤을때 각각의 한 점에서 다른 한점 까지의 거리들 중에서 가장 작은 값들의 합계를 구하는 것이다. 즉, 예제 입력1의 경우를 보자면 1번색깔의 점들은 0,3,5가 있다
1) 0의 경우 3이 제일 가까움 sum = 3
2) 3의 경우 0보다는 5가 더 가까움 sum = 3 + 2
3) 5의 경우 3이 제일 가까움 sum = 3 + 2 + 2
2번 색깔의 점들은 1과 4가 있으며, 2번 색깔의 경우도 위와 마찬가지이다
1) 1의 경우 4가 제일 가깝다. sum = 3 + 2 + 2 + 3
2) 4의 경우 1이 제일 가깝다. sum = 3 + 2 + 2 + 3 + 3
따라서 sum = 3 + 2 + 2 + 3 + 3 = 13이다.
파이썬의 경우 sort 기능으로 2차원 배열을 간단하게 정렬했지만 C에서는 방법을 몰라서 구글링하여 조금 조사하였다.
( 2차원 배열이기 떄문에 C에서 sort(arr,arr+N) 이라고만 적어으면 오류가 발생! )
vector<vector> arr(N + 1); => N개의 색깔별로 점들을 저장할 수 있는 2차원 배열을 선언.
for (int i = 0; i < N; i++) { => push_back을 이용해 arr[y]에 점들을 저장한다.
scanf("%d %d", &x, &y);
arr[y].push_back(x);
color[y]++; // 같은 색의 점들이 각각 몇개 있는지 표시하기 위한 배열
}
sort(arr[i].begin(), arr[i].end()) => 각각의 색깔별로 점들을 정렬해준다.
<C 코드>
#include<stdio.h>
#include<vector>
#include<algorithm>
using namespace std;
int color[5001];
int main() {
int x, y; // x좌표와 y색깔
int N = 0; // 점의 갯수
scanf("%d", &N);
vector<vector<int>> arr(N + 1); // 2차원 배열
int distance = 0; // 거리의 합
for (int i = 0; i < N; i++) {
scanf("%d %d", &x, &y);
arr[y].push_back(x); // 색깔별로 점들 분류하기
color[y]++; // 같은 색의 점들이 각각 몇개 있는지 표시하기 위한 배열
}
for (int i = 1; i <= N; i++) {
sort(arr[i].begin(), arr[i].end()); // 색깔별로 2차원 배열 정렬하기
}
for (int i = 1; i <= N; i++) {
if (arr[i].size() == 0) continue; // 해당 색깔의 점이 0이라면 건너뛰기
for (int j = 0; j < color[i]; j++) {
if (j == 0) distance += arr[i][1] - arr[i][0]; // 맨 처음부분 연산
else if (j == color[i] - 1) distance += arr[i][color[i] - 1] - arr[i][color[i] - 2]; // 맨 끝부분 연산
else {
int a = arr[i][j - 1];
int b = arr[i][j + 1];
distance += min(arr[i][j] - a, b - arr[i][j]); //양 옆의 거리들중 작은 값 더하기
}
}
}
printf("%d\n", distance);
}
<Python 코드>
def fcn(arr):
sum = 0
for i in range(len(arr)):
if i == 0:
sum += arr[1] - arr[0]
elif i == len(arr) - 1:
sum += arr[len(arr) - 1] - arr[len(arr) - 2]
else:
if arr[i + 1] - arr[i] >= arr[i] - arr[i - 1]:
sum += arr[i] - arr[i - 1]
else:
sum += arr[i + 1] - arr[i]
return sum
ans = 0
n = int(input())
arr = []
for i in range(n):
a, b = map(int, input().split())
arr.append([b, a])
arr.sort()
l = arr[-1][0]
for i in range(1, l+1):
x = []
for j in range(n):
if arr[j][0] == i:
x.append(arr[j][1])
ans += fcn(x)
print(ans)
https://www.acmicpc.net/problem/15970
15970번: 화살표 그리기
직선 위에 위치를 나타내는 0, 1, 2, ...와 같은 음수가 아닌 정수들이 일정한 간격으로 오른쪽 방향으로 놓여 있다. 이러한 위치들 중 N개의 위치에 하나씩 점들이 주어진다(<그림 1>). 주어진 점들의 위치는 모두 다르다. 두 점 사이의 거리는 두 점의 위치를 나타내는 수들의 차이이다. <그림 1>에서는 4개의 점이 주어지고 점 a와 b의 거리는 3이다. <그림 1> 각 점은 N개의 색깔 중 하나를 가진다. 편의상, 색깔은 1부터 N까지의 수로 표
www.acmicpc.net
'🧩PS > 🥈Nomal' 카테고리의 다른 글
| [C/C++/Python] 백준 2596번 비밀편지 (0) | 2020.05.02 |
|---|---|
| [C/C++/Python] 백준 2864번 5와6의 차이 (0) | 2020.04.25 |
| [C/C++/Python] 백준 16769번 Mixing Milk (0) | 2020.04.24 |
| [C/C++] 백준 1373번 2진수 8진수 (0) | 2020.04.13 |
| [ C/C++] 백준 1212번 8진수 2진수 (0) | 2020.04.13 |