

<코드>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
int N, M;
int u, v;
queue<int> q;
vector<int> node[50001];
bool check[50001];
int parent[50001];
int depth[50001];
int LCA(int u, int v)
{
// v가 u보다 더 깊은 노드로 세팅
if (depth[u] > depth[v]) swap(u, v);
// 두 노드의 깊이가 같아질때까지 v노드는 위로 거슬러 올라감
while (depth[u] != depth[v]) v = parent[v];
// 두 노드가 같아질때 까지 위로 거슬러 올라감
while (u != v)
{
u = parent[u];
v = parent[v];
}
return u; // LCA 리턴
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> N;
// 해당노드에 연결된 노드 push
for (int i = 0; i < N-1; i++)
{
cin >> u >> v;
node[u].push_back(v);
node[v].push_back(u);
}
check[1] = true;
q.push(1); // 트리의 루트
while (!q.empty())
{
int x = q.front(); // 부모 노드
q.pop();
for (int i = 0; i < node[x].size(); i++)
{
if (!check[node[x][i]]) // 현재노드를 방문한적 없다면
{
depth[node[x][i]] = depth[x] + 1; // 깊이 +1
check[node[x][i]] = true; // 방문표시
parent[node[x][i]] = x; // 부모노드 입력
q.push(node[x][i]); // 큐에 추가
}
}
}
cin >> M;
for (int i = 0; i < M; i++)
{
cin >> u >> v;
cout << LCA(u, v) << '\n';
}
}
풀이 방법
LCA는 Lowest Common Ancestor의 약자이며 최소 공통 조상이라는 의미를 가지고 있습니다.

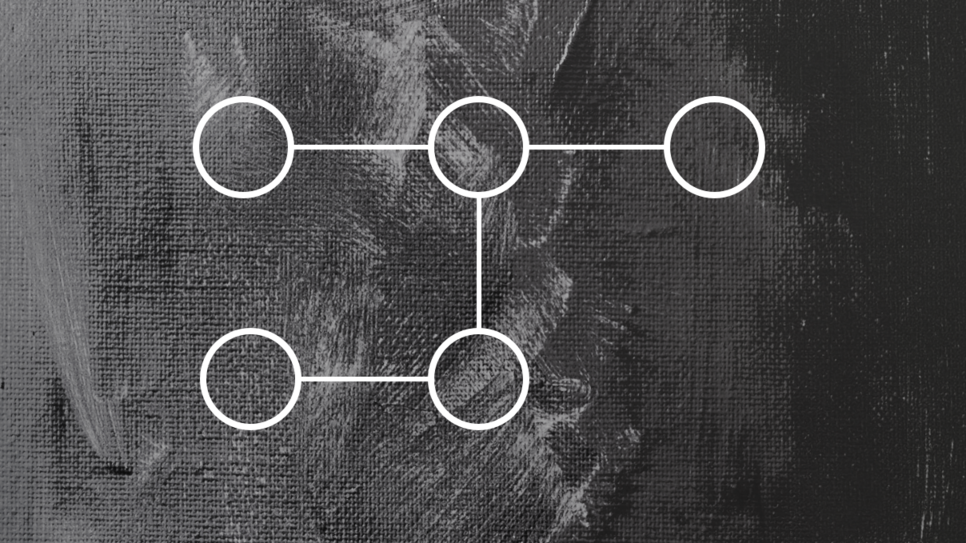
예제 입력 1의 입력을 트리로 표현을 해봤습니다. 루트 노드는 1번입니다. 간단하게 LCA를 구해보면,

11번 노드와 10번 노드의 LCA는 2번 노드입니다.

마찬가지로 2번 노드와 14번 노드의 LCA는 1번 노드가 됩니다.
코드를 살펴보면
<변수 설명>
vector<int> node[50001]; 해당 인덱스의 노드와 연결된 노드들의 정보를 나타냅니다. 예를 들어 node[3] = {4, 7, 11}은 3번 노드가 4, 7, 11번 노드와 연결되어 있다는 뜻입니다.
bool check[50001]; 해당 노드에 방문을 했는지 표시합니다.
int parent[50001]; 해당 인덱스의 노드의 부모 노드 정보를 나타냅니다. 예를 들어 parent[3] = 11은 3번 노드의 부모 노드가 11번 노드라는 의미입니다.
int depth[50001];해당 인덱스의 노드의 깊이를 뜻합니다. 쉽게 말해 루트에서 떨어진 거리라고도 표현할 수 있습니다.
<코드 설명>
cin >> N;
// 해당노드에 연결된 노드 push
for (int i = 0; i < N-1; i++)
{
cin >> u >> v;
node[u].push_back(v);
node[v].push_back(u);
}먼저 N-1개의 입력이 들어오면 각각의 노드에 해당 노드와 연결된 노드들을 push 하게 됩니다.
예를 들어 입력이 "1 2"와 "1 3"이 들어오게 된다면,
node[1] = {2, 3}
node[2] = {1}
node[3] = {1}
과 같이 저장되게 됩니다.
check[1] = true;
q.push(1); // 트리의 루트
while (!q.empty())
{
int x = q.front(); // 부모 노드
q.pop();
for (int i = 0; i < node[x].size(); i++)
{
if (!check[node[x][i]]) // 현재노드를 방문한적 없다면
{
depth[node[x][i]] = depth[x] + 1; // 깊이 +1
check[node[x][i]] = true; // 방문표시
parent[node[x][i]] = x; // 부모노드 입력
q.push(node[x][i]); // 큐에 추가
}
}
}이제 루트 노드인 1번을 방문 표시를 해주고 큐에 삽입합니다. 그런 다음 while문으로 진입하여 BFS를 통해 해당 노드와 연결된 노드들의 부모 노드, 방문 여부, 깊이를 표시해주고 큐에 추가합니다.

예를 들어 위의 트리에서 node[1] = {2, 3}입니다. 따라서 node[1].size() 는 2개이고 먼저 node[1]의 첫 번째 원소인 node[1][0]의 깊이는 부모 노드의 깊이 + 1을 해주고, 방문 표시를 한 다음, parent 배열에서 parent[node[1][0]]의 부모는 x라고 저장을 해줍니다. 그리고 큐에 node[1][0]을 추가해줍니다. 이런 식으로 큐에 원소가 하나도 없을 때까지 while문을 돌아서 parent 배열을 완성시켜 줍니다.
cin >> M;
for (int i = 0; i < M; i++)
{
cin >> u >> v;
cout << LCA(u, v) << '\n';
}이제 노드 2개를 입력받아 LCA함수에 파라미터로 보내서 함수를 호출합니다.
int LCA(int u, int v)
{
// v가 u보다 더 깊은 노드로 세팅
if (depth[u] > depth[v]) swap(u, v);
// 두 노드의 깊이가 같아질때까지 v노드는 위로 거슬러 올라감
while (depth[u] != depth[v]) v = parent[v];
// 두 노드가 같아질때 까지 위로 거슬러 올라감
while (u != v)
{
u = parent[u];
v = parent[v];
}
return u; // LCA 리턴
}처음에 u노드의 깊이가 v노드의 깊이보다 더 깊을 때 swap을 해주는 이유는 편의성을 위해서 swap을 해주는 것입니다.
예를 들어 u와 v의 입력이 "14 5"라고 한다면, 14번 노드의 깊이가 5번 노드의 깊이보다 더 깊으므로
u, v = "14 5"에서 "5 14"로 변경해줍니다.

그런 다음 두 노드의 깊이가 같지 않으므로 v노드는 자신의 부모 노드로 거슬러 올라갑니다.

이제 노드의 깊이를 서로 맞췄으므로 두 노드가 같아질 때까지 한 단계씩 부모로 거슬러 올라가 보겠습니다.


따라서 5번 노드와 14번 노드의 LCA(최소 공통 조상)은 1번 노드가 됩니다.
11437번: LCA
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
'🧩PS > 🥈Nomal' 카테고리의 다른 글
| [C/C++] 백준 5585번 - 거스름돈 (0) | 2020.12.29 |
|---|---|
| [C/C++] 백준 13458번 - 시험 감독 (0) | 2020.12.29 |
| [C/C++] 백준 10942번 - 팰린드롬? (DP) (0) | 2020.12.28 |
| [C/C++] 백준 1655번 - 가운데를 말해요 (최대 힙, 최소 힙) (0) | 2020.12.28 |
| [C/C++] 백준 11286번 - 절댓값 힙 (우선순위 큐) (0) | 2020.12.27 |