반응형

<코드>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 1024
int table[MAX+1][MAX+1];
int dp[MAX+1][MAX+1];
int N, M, ans;
int x;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
int x1, x2, y1, y2;
cin >> N >> M;
for (int i = 1; i <= N; i++)
for (int j = 1; j <= N; j++)
{
cin >> x;
if (i == 1 && j == 1) dp[i][j] = x;
else if (i == 1)
{
dp[i][j] = x + dp[i][j - 1];
}
else if (j == 1)
{
dp[i][j] = x + dp[i - 1][j];
}
else
{
dp[i][j] = x + dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1];
}
}
for (int i = 0; i < M; i++)
{
cin >> x1 >> y1 >> x2 >> y2;
ans = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];
cout << ans << '\n';
}
}
풀이 방법
dp[i][j] : 1행 1열부터 i행 j열까지의 누적 합

<기본 아이디어>





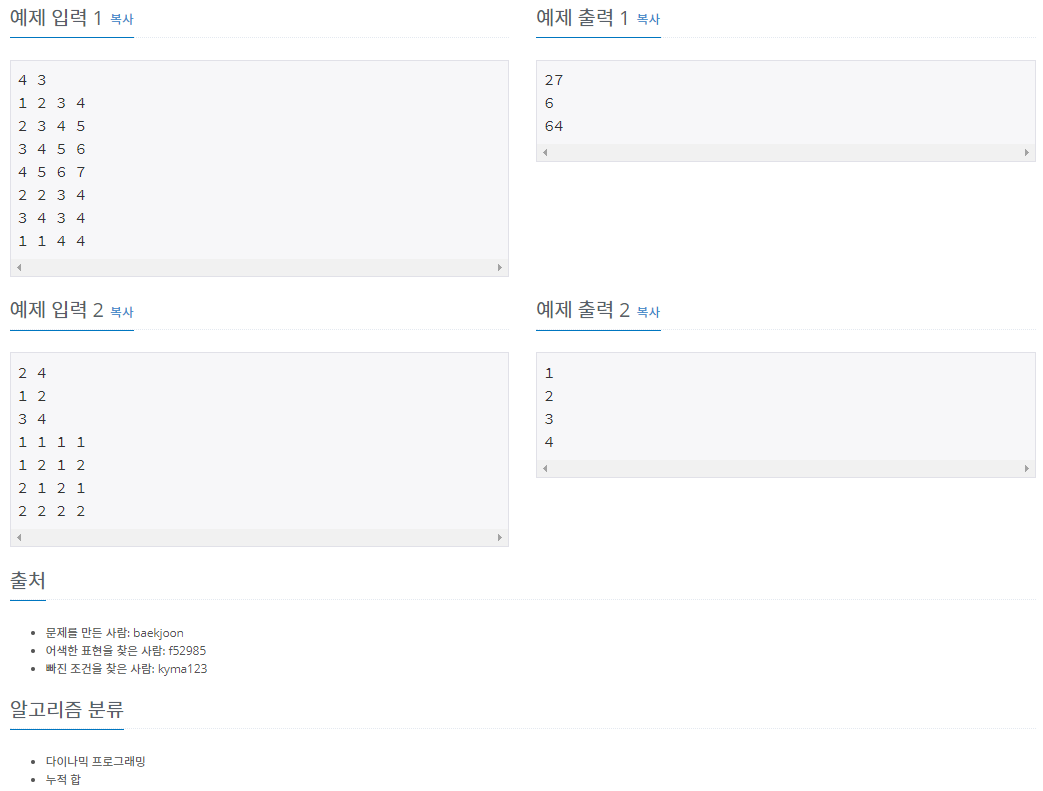
이번 문제는 dp를 통해서 구한 구간(1,1)에서 임의의 (i, j) 구간까지의 누적합을 이용해서 풀 수 있습니다. 푸른색의 영역을 구하기 위해서는 위의 그림과 같이 1번 영역에서 2,3번 영역을 빼주는데, 이때 4번영역을 중복으로 뺏기 때문에 4번 영역을 더해줍니다. 그렇다면 (x1,y1)~(x2,y2)의 구간합을 구할 수 있게 됩니다.
1번 영역 dp[x2][y2]
2번 영역 dp[x1-1][y2]
3번 영역 dp[x2][y1-1]
4번 영역 dp[x1-1][y1-1]
(x1,y1)~(x2,y2)의 구간합 = dp[x2][y2] - dp[x1-1][y2]- dp[x2][y1-1]+ dp[x1-1][y1-1]
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
반응형
'🧩PS > 🥈Nomal' 카테고리의 다른 글
| [C/C++] 백준 3976번 - 역습 (DP) (1) | 2021.01.19 |
|---|---|
| [C/C++] 백준 16953번 - A → B (2) | 2021.01.17 |
| [C/C++] 백준 1074번 - Z (분할정복) (0) | 2021.01.17 |
| [C/C++] 백준 17946번 - 피자는 나눌 수록 커지잖아요 (0) | 2021.01.17 |
| [C/C++] 백준 7489번 - 팩토리얼 (0) | 2021.01.17 |