
소수의 정의는 '1과 자기 자신으로밖에 나누어 떨어지지 않고 자기 자신의 곱셈의 역수가 없는 1 이외의 정수'입니다. 대표적인 소수를 예로 들자면 2, 3, 5 ,7 ,11, 13, 17,.... 등등이 있습니다. 이번 포스팅은 소수를 구하는 코드를 C언어를 사용하여 구현해보려 합니다.
<for문 Code>
#include<stdio.h>
int main(void)
{
int cnt ,num;
scanf("%d", &num);
for (int i = 2; i <= num; i++)
{
cnt = 0;
for (int j = 2; j <= i; j++)
{
if (i % j == 0)
cnt++;
}
if (cnt == 1) // 나눠지는 수가 1개 뿐인 경우
printf("%d ", i);
}
}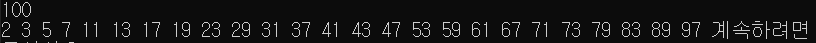
<Recursion Code>
#include<stdio.h>
int recursion(int N, int i)
{
int result = 0;
if (i <= 0) return 0;
if (N % i == 0) result = 1;
else result = 0;
result += recursion(N, i - 1);
return result;
}
int main(void)
{
int num, cnt = 0;
scanf("%d", &num);
for (int i = 0; i < num; i++)
{
cnt = recursion(i, i);
if (cnt == 2) printf("%d ", i);
}
return 0;
}
<에라토스테네스의 체>

<알고리즘>
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
그림의 경우, (11의 제곱 = 121>120) 이므로 11보다 작은 수의 배수들만 지워도 충분합니다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수입니다.
예를들어 100의 인수들을 살펴보면
1 * 100 = 100
2 * 50 = 100
4 * 25 = 100
5 * 20 = 100
10 * 10 = 100
20 * 5 = 100
25 * 4 = 100
50 * 2 = 100
100 * 1 = 100
총 9 개 이며 인수들은 루트(100)의 값을 넘어가지 않는데,
에라토스테네스의 체를 이용해 1~n까지의 소수를 알고 싶다면, n까지 모든 수의 배수를 다 나눠 볼 필요는 없습니다.
만약 어떤 수가 m=ab 이라면 a와 b 중 적어도 하나는 루트(n) 이하입니다. 즉 n보다 작은 합성수 m은 루트(n) 보다 작은 수의 배수만 체크해도 전부 지워진다는 의미이므로, 이하의 수의 배수만 지우면 됩니다.
<에라토스테네스의 체 Code>
#include<stdio.h>
#include<math.h>
int main(void)
{
int num;
int cnt = 0;
int arr[10000];
scanf("%d", &num);
for (int i = 2; i <= num; i++)
{
arr[i] = i;
}
for (int i = 2; i <= sqrt(num); i++)
{
if (arr[i] == 0) continue;
for (int j = 2 * i; j <= num; j += i)
{
arr[j] = 0;
}
}
for (int i = 2; i <= num; i++)
{
if (arr[i] != 0) printf("%d ", arr[i]);
}
}
확실히 에라토스테네스의 체 방식이 반복문보다 훨씬 빠른데 백문이 불여일견이므로 각각의 코드 실행시간을 10번씩 재보았습니다.
<반복문으로 1~100000 사이의 소수 찾기>

<에라토스테네스의 체 방식으로 1~100000 사이의 소수 찾기>

12.3 sec VS 0.45 sec
프로그래밍 공부를 처음 시작할때는 "그냥 for문이랑 if문만 알면 되겠지~ 컴퓨터인데 몇초 차이 나겠어?" 라고 생각했던 것들이 깊이 공부를 하면 할수록 알고리즘과 시간복잡도, 최적화가 얼마나 중요한지 깨닫게 됩니다.
'🟦C++' 카테고리의 다른 글
| [C/C++] endl 와 \n의 속도차이 (0) | 2020.06.06 |
|---|---|
| [C/C++] 배열 & 포인터 예제 (0) | 2020.05.15 |
| [C++] 명품 C++ Programming 2장 연습, 실습 문제풀이 (6) | 2020.05.14 |
| [C/C++] 최대공약수(GCD), 최소공배수(LCM) (유클리드 호제법) (0) | 2020.04.12 |
| [ C/C++] 순열(Permutation)과 조합(Combination) 알고리즘 구현하기 (0) | 2020.04.10 |