
<알고리즘의 수학적 표기 방법>
세상에는 무수히 많은 알고리즘이 존재한다. 알고리즘의 성능을 판단할 때 적용된 시스템, 컴파일러 종류, 사용 환경 등등의 변수가 있으며 알고리즘의 시간 측정이나 메모리 사용 여부만으로는 무리가 있다. 그리고 정렬 알고리즘, 검색 알고리즘, 압축 및 암화화 알고리즘 등 복잡한 알고리즘의 경우 그것이 최선 혹은 최악의 경우인지에 따라 성능이 달라질 수 있다.
그러한 알고리즘의 성능을 평가하는 확실한 방법은 무엇일까? 이를 위해 알고리즘을 수학적으로 연구하는 학자들에 의해 만들어진 표기 방법이 있다.
가령 실수를 다루는 함수 T(N)과 f(N)이 있다고 가정하자
1. T(N) <= cf(N), N >= N1이라는 두 조건을 만족하는 상수 c와 N1이 존재한다면 T(N) = O(f(N))이다.
2. T(N) >= cf(N), N >= N1이라는 두 조건을 만족하는 상수 c와 N1이 존재한다면 T(N) = Ω(f(N))이다.
3. T(N) = O(f(N))이라는 두 조건을 만족하는 상수 c와 N1이 존재하며 T(N) = Ω(f(N))이라는 조건을 만족하는 상수 c2와 N1이 존재할 때 T(N) =Θ(f(N))이라고 한다.
여기서 1의 경우를 빅오(O) 표기법(Big-O Notation)이라고 한다. 알고리즘 성능 평가 방법 중 가장 많이 사용하며 최고와 최악의 성능 중 최악의 성능을 측정하는 방법이다. 2는 1과 반대로 오메가(Ω) 표기법(Omega Noation)이라고 하며 알고리즘의 성능이 최고인 경우 측정하는 표기법이다. 그다지 자주 사용하지 않는다. 마지막 3의 경우는 세타(Θ) 표기법(Theta Notation)이라고 하며 최고/최악의 성능이 아니라 정확한 알고리즘 성능을 측정하는 방법이다. 세타 표기법의 경우 가장 좋은 성능 표기법이라고 할 수 있지만 실제로 알고리즘의 성능을 이처럼 표기하기는 어렵다.
예시 - 1~100까지의 합을 구하는 프로그램
#include<stdio.h>
void main()
{
int sum = 0;
int i;
for (i = 1; i < 100; i++)
{
sum = sum + i;
}
printf("1 부터 100 까지의 합 : %d\n", sum);
}1. 헤더 파일은 알고리즘의 성능에 영향을 주지 않는다.
2. 함수 진입과 함수 반환은 알고리즘의 성능에 영향을 주지 않는다.
3. 프로그램은 첫 번째부터 마지막 행까지 차례대로 진행된다.
| 알고리즘 성능에 영향을 주는 코드 | 실행 횟수 |
| int sum = 0; | 1회 |
| int i; | 1회 |
| for (i = 1; i < 100; i++) | 101회 |
| sum = sum + i; | 100회 |
| printf("1 부터 100 까지의 합 : %d\n", sum); | 1회 |
| 합계 | 204회 |
위 표의 실행 횟수를 빅오 표기법으로 나타내면 다음과 같다.
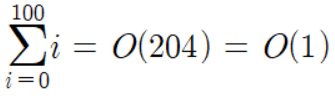
204회 실행되더라도 204라는 상수의 존재는 알고리즘의 성능에 아무런 영향을 끼치지 못한다. 따라서 빅오 표기법으로 위 알고리즘을 나타내면 O(1)이 된다. O(1)은 알고리즘의 성능이 고정적이라는 의미이다.
그럼 이번에는 1부터 N까지 1을 계속 더하는 경우를 생각해보자.
for (i = 1; i < N; i++)
{
sum = sum + i;
}N의 값에 따라 for문의 반복 횟수가 결정되며 이는 곧 알고리즘 성능과 직결되는 문제이다. 따라서 1부터 N까지 특정 숫자를 더하는 프로그램을 수학식으로 나타낸 후 이를 빅오 표기법으로 나타내면 다음과 같다.
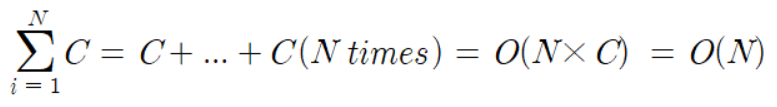
이와 같이 빅오 표기법은 처리해야 할 데이터양에 대한 실행 시간을 수학적으로 계산해 알고리즘의 성능을 평가한다.
<대표적인 시간 복잡도>
O(1) : 처리해야 할 데이터양과 상관없이 항상 일정한 실행 시간을 갖는 알고리즘.
O(logN) : 처리해야 할 데이터 양이 증가할수록 실행 시간도 약간씩 증가하는 알고리즘. 단, 실행 시간의 증가폭이 로그함수의 그래프를 갖기 때문에 급격히 증가하지는 않는다. 일반적으로 효율 높은 검색 알고리즘의 성능이 이에 해당한다.
O(N) : 처리해야 할 데이터양과 비례해 실행시간도 증가하는 알고리즘.
O(NlogN) : 처리해야 할 데이터 양보다 실행 시간이 좀 더 빠르게 증가하는 알고리즘. 일반적으로 정렬 알고리즘의 성능이 이에 해당한다.
O(N^2) : 보통 반복문이 2번 중첩된 경우의 알고리즘. 이와 같은 알고리즘은 처리해야 할 데이터양이 증가할수록 데이터양의 제곱만큼 실행시간이 증가한다.
O(N^3) : 반복문이 3번 중첩된 알고리즘. 처리해야 할 데이터양이 증가하면 실행 시간은 그 세제곱만큼 증가하며 좋은 알고리즘이라고 볼 수 없다.
O(2^N) : 데이터양 증가에 따라 2^N 만큼 실행시간이 증가하는 알고리즘.
출처 - 프로그래머의 취업, 이직을 결정하는알고리즘 문제 풀이 전략 (한빛미디어)
'🗝️Algorithm' 카테고리의 다른 글
| [PYTHON] the smallest set of unit-length closed intervals (0) | 2020.11.13 |
|---|---|
| [C/C++] 팬케이크 정렬 알고리즘 (0) | 2020.11.13 |
| [C/C++] 가장 작은 개수의 동전으로 n원을 만드는 알고리즘 구현 (greedy) (0) | 2020.11.13 |
| [ALGORITHM] 알고리즘 분석과 최적화 (0) | 2020.02.19 |
| [ALGORITHM] 알고리즘의 정의 (0) | 2020.02.16 |