
알고리즘의 성능을 평가하기 위해 현실적으로 시간의 효율성, 공간의 효율성, 코드의 효율성으로 평가되어야 하지만 (실행환경 - 운영체제, 하드웨어 등등은 배제) 현실적으로 공간의 효율성, 코드의 효율성 조차 모두 평가의 요소로 활용하기는 어렵다. 예를 들어 코드의 효율성은 프로그래밍 언어에 따라 달라질 수 있으며 공간의 효율성 역시 프로그램을 실행해서 사용량을 측정해보기 전에는 알고리즘이 얼마나 많은 메모리 혹은 기타 저장 공간을 사용하게 하는지 정확히 알기 어렵다. 또한 프로그램 실행과는 무관한 운영체제의 저장공간 관리 방식도 공간의 효율성에 영향을 미치므로 알고리즘의 객관적인 성능을 평가하는 요소로 사용하기 어렵다.
결국 알고리즘의 성능을 평가하는 가장 현실적인 항목은 시간의 효율성인데 알고리즘이 어느 정도의 시간을 소비하는지 빅오 표기법으로 나타내 보면 객관적이고 수학적인 알고리즘의 성능 평가가 가능하다.
<C에서 자주 사용하는 문법 요소들을 빅오 표기법으로 나타내는 방법>
1. 반복문은 최대 반복 횟수로 계산한다.
for (i = 0; i <= 100; i++)
{
sum += 1;
}1부터 100까지 총 11번을 반복한다. 이경우 빅오 표기법으로 나타내면 O(100)인데 100은 상수이므로 결국 위의 반복문의 빅오 표기법은 O(1)이 된다. 100을 N으로 바꾸면 빅오 표기법은 O(N)이 된다.
2. 중첩된 반복문은 중첩 문의 각각의 최대 반복 횟수를 곱해서 계산한다.
for (i = 0; i <= N; i++)
{
for (j = 0; j <= N; j++)
{
sum += 1;
}
}위의 코드를 빅오 표기법으로 나타내면 O(N*N) = O(N²)이 된다. 마찬가지로 아래와 같은 경우는 O(N*N이 된다.
for (i = 0; i <= N; i++)
{
for (j = 0; j <= N; j++)
{
for (k = 0; k <= N; k++)
{
sum += 1;
}
}
}
3. 반복문이 떨어져서 2개 이상 있는 경우는 그중 가장 큰 값으로 계산한다.
for (i = 0; i <= N; i++)
{
sum += 1;
}
for (i = 0; i <= N; i++)
{
for (j = 0; j <= N; j++)
{
sum += 1;
}
}이 경우 첫 번째 for문과 두 번째 중첩 for문은 별개의 for문이다. 따라서 각각 빅오 표기법으로 나타내면 O(N), O(N²)이 된다. 이 중에서 두 번째 for문의 빅오 표기가 더 큰 차수이므로 이경우는 빅오 표기법으로 나타내면 O(N²)이다.
4. if-else문은 알고리즘 성능에 영향을 미치지 않는다.
프로그램 안에서 가장 빈번하게 사용되는 구문 중에 하나는 if-else 구문이다. 그러나 if-else문은 알고리즘의 성능에 영향을 미치지 않는다.
5. 재귀 호출은 풀어서 계산한다.
int Fact(int N)
{
if (N <= 1)
return 1;
else
return N * Fact(N - 1);
}얼핏 보면 if-else문에 재귀 호출까지 섞여있어 복잡해 보이지만 앞에 설명한 것처럼 if-else문은 알고리즘의 성능에 영향을 미치지 않고 결국 남은 것은 else문 안에서 함수를 재귀 호출한 returnreturn N * Fact(N - 1); 뿐이다.
위의 재귀 호출은 다음처럼 표현될 수 있다.
N*(N-1)*(N-2)*......*3*2*1
결국 N부터 1까지의 곱인데 사실상 반복 횟수는 N회 이므로 빅오 표기법으로 나타내면 위 팩토리얼 함수는 O(N)이 된다.
알고리즘의 성능에 제일 중요한 요소는 시간이다. 같은 기능을 실행해 실행시간을 얼마나 줄일 수 있느냐에 따라 해당 알고리즘이 뛰어난 알고리즘인지 쓸모없는 알고리즘인지 판단할 수 있다.
그러나 현실적으로 모든 알고리즘을 구현해서 직접 실행시켜보기도 어려울뿐더러 알고리즘의 각각의 실행 시간을 계속 확인한다는 것도 현실성이 없다. 1, 2분 정도가 아니라 1달이 걸릴지 2달이 걸릴지 모르기 때문이다. 결국 알고리즘의 성능을 증명하는 가장 빠르고 정확한 방법이 바로 수학적 분석이다.
그렇다면 빅오 표기법을 이용하여 프로그램을 수학적으로 분석해봅시다.
아래의 코드는 하나의 배열에 저장된 1부터 N까지의 요소중 첫 번째 요소부터 차례대로 더했을 때 합이 가장 는 수를 찾아내는 부분 수열의 합을 구하는 프로그램이다. 예를 들어 arr = [4, -1, 5, -2]와 같이 배열에 4개의 데이터가 존재한다고 하면 이중 합이 가장 큰 수는 4 -1 + 5를 더했을 때이다.
<부분 수열의 합을 구하는 프로그램>
#include<stdio.h>
int MaxSum(int);
void Init(void);
int arr[100];
int MaxSum(int N)
{
int Sum, Max, i, j, k;
Sum = Max = 0;
for (i = 0; i < N; i++)
{
for (j = 0; j < N; j++)
{
Sum = 0;
for (k = 0; k < N; k++)
{
Sum += arr[k];
if (Sum > Max)
{
Max = Sum;
}
}
}
}
return Max;
}
void Init()
{
int i;
for (i = 0; i < 100; i++)
{
arr[i] = 100 - i;
}
}
void main()
{
int ret;
Init();
ret = MaxSum(10);
printf("%d\n", ret);
}
먼저 3개의 for문을 시그마 연산으로 나타내면 다음과 같다.

그리고 가장 안쪽의 for문은 시그마 연산으로 다음과 같이 나타낼 수 있다.
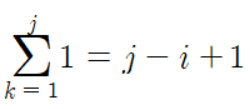
제어 변수 k는 i부터 j까지 반복되므로 변수 i와 j는 상수 취급한다. 따라서 (최댓값 - 최솟값 + 1)이라는 식으로 나타낼 수 있다. 그리고 앞의 두 결과를 포함해서 시그마 연산으로 나타내면 다음과 같다.
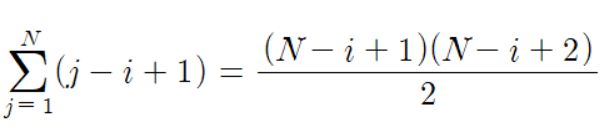
결국 첫 번째 for문 기준으로 시그마 연산은 다음처럼 나타낼 수 있다.

위의 시그마 연산을 계산하면 다음과 같은 과정을 거친다.

따라서 위의 시그마 연산의 결과를 빅오 표기법으로 나타내면 다음과 같다.

즉, 빅오 표기법으로 표현하면 O(N³)이 되는 것이다.
알고리즘의 성능을 좀 더 끌어올리는 최적화는 이론적으로는 최악의 성능을 더 좋아지게 수정해 결구 전체적인 성능을 향상하는 것이다. 즉, O(N³)라면 더 최적화시켜 O(N²)으로, O(N²)의 경우 O(NlogN)에서 더 나아가 O(N)으로 향상할 수가 있다.
<O(N²)의 성능으로 향상시킨 부분 수열의 합을 구하는 프로그램>
#include<stdio.h>
int MaxSum(int);
void Init(void);
int arr[100];
int MaxSum(int N)
{
int Sum, Max, i, j, k;
Sum = Max = 0;
for (i = 0; i < N; i++)
{
Sum = 0;
for (j = i; j < N; j++)
{
Sum += arr[j];
if (Sum > Max)
{
Max = Sum;
}
}
}
return Max;
}
void Init()
{
int i;
for (i = 0; i < 100; i++)
{
arr[i] = 100 - i;
}
}
void main()
{
int ret;
Init();
ret = MaxSum(10);
printf("%d\n", ret);
}
첫번째 코드에서 3 중첩 for문을 2충접 for문으로 수정하였다. 변수 N을 10이나 100으로 해서는 속도 차이를 느끼지 못하겠지만 만약 변수 N 값이 10000이나 1000000 혹은 그 이상이 되었다고 가정해보면 O(N²)과 O(N³)의 차이는 엄청날 것이다.
이처럼 알고리즘을 최적화하려면 알고리즘의 전체 성능에 관한 빅오 표기법을 먼저 파악하고 해당 빅오 표기법의 성능을 높이는 방향으로 코드를 수정하는 것이 가장 좋은 방법이다.
출처 - 프로그래머의 취업, 이직을 결정하는알고리즘 문제 풀이 전략 (한빛미디어)
'🗝️Algorithm' 카테고리의 다른 글
| [PYTHON] the smallest set of unit-length closed intervals (0) | 2020.11.13 |
|---|---|
| [C/C++] 팬케이크 정렬 알고리즘 (0) | 2020.11.13 |
| [C/C++] 가장 작은 개수의 동전으로 n원을 만드는 알고리즘 구현 (greedy) (0) | 2020.11.13 |
| [ALGORITHM] 빅오 표기법 (Big-O Notation) 알고리즘의 시간 복잡도 (0) | 2020.02.17 |
| [ALGORITHM] 알고리즘의 정의 (0) | 2020.02.16 |