<코드>
#include<iostream>
#include<algorithm>
using namespace std;
#define MOD 1000000
int num[100001], pos[100001];
int n, x, ans;
int pole1, pole2, pole3;
void cal(int n) // 2의 ?승들을 저장하기 위한 함수
{
num[0] = 1;
for (int i = 1; i <= n; i++)
num[i] = (num[i - 1] * 2) % MOD;
}
void hanoi(int disc, int to) // to는 옮겨야 할 곳
{
if (disc == 0) return;
int now = pos[disc]; // 현재 원판의 위치
int sub; // 보조 막대기
for (int i = 1; i <= 3; i++)
if (now != i && to != i)
sub = i;
if (now == to) hanoi(disc - 1, to);
else
{
ans = (ans + num[disc - 1]) % MOD;
hanoi(disc - 1, sub);
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
cal(n);
cin >> pole1 >> pole2 >> pole3;
// 원판의 위치 기록
for (int i = 0; i < pole1; i++)
{
cin >> x;
pos[x] = 1;
}
for (int i = 0; i < pole2; i++)
{
cin >> x;
pos[x] = 2;
}
for (int i = 0; i < pole3; i++)
{
cin >> x;
pos[x] = 3;
}
hanoi(n, pos[n]);
cout << pos[n] << '\n';
cout << ans << '\n';
}
풀이 방법
<기본 아이디어>
1. 최소의 이동으로 모든 원판을 한 막대기로 옮기려면 가장 큰 원판이 있는 막대기로 모든 원판을 옮겨야 합니다.
2. (i)크기의 원판을 (i+1)크기의 원판 위로 옮기기 위해서는 1~(i-1)크기의 원판들을 한 곳에 모두 옮겨놔야 합니다.
(아래에 그림으로 자세하게 설명하겠습니다.)
3. 1~(i-1)크기의 원판들을 잠시 옮겨놓는 막대를 보조 막대(코드에선 변수명 sub)라고 지칭하겠습니다.
<코드설명>
void cal(int n) // 2의 ?승들을 저장하기 위한 함수
{
num[0] = 1;
for (int i = 1; i <= n; i++)
num[i] = (num[i - 1] * 2) % MOD;
}cal함수는 n이 최대 10만이기 때문에 2의 i승들을 기록하기 위한 함수입니다.
void hanoi(int disc, int to) // to는 옮겨야 할 곳
{
if (disc == 0) return;
int now = pos[disc]; // 현재 원판의 위치
int sub; // 보조 막대기
for (int i = 1; i <= 3; i++)
if (now != i && to != i)
sub = i;
if (now == to) hanoi(disc - 1, to);
else
{
ans = (ans + num[disc - 1]) % MOD;
hanoi(disc - 1, sub);
}
}처음 시작은 hanoi(n, pos[n])으로 시작하게 됩니다. 즉, hanoi(제일 큰 원판, 원판의 위치)이며, 재귀 함수에서 disc변수가 0이 되면 함수는 종료됩니다.
now는 현재 원판의 위치이고 sub는 현재 원판을 to로 옮기기 위해 나머지 원판을 모아 놓을 막대기 번호입니다.
for문으로 (옮겨야 할 곳 & 현재 원판의 위치)를 제외한 곳을 찾아서 sub로 지정합니다.
현재 원판 크기를 disc라 할 때 만약 현재 원판의 위치가 옮겨야 할 곳(to)에 있다면 다음 원판(disc-1)으로 넘어가고,
현재 원판의 위치가 옮겨야 할 곳(to)에 있지 않다면 다음 원판(disc-1)을 보조(sub) 막대로 옮겨야 합니다.
(그래야 disc 원판을 disc+1 원판 위로 옮길 수 있기 때문!)
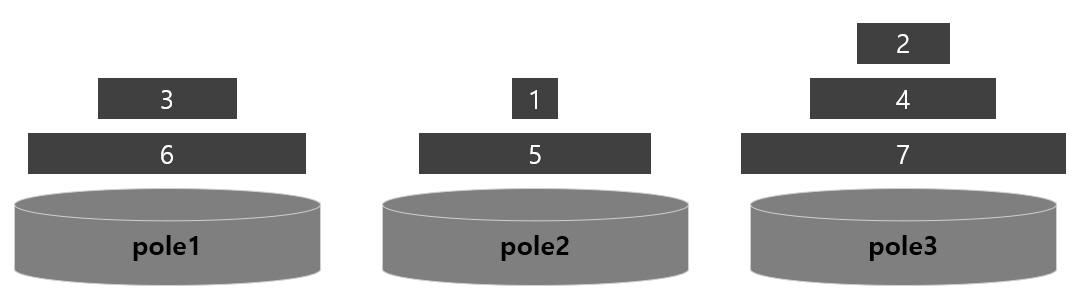
<입력 예시>
7
2 2 3
6 3
5 1
7 4 2
먼저 위의 예시에서 가장 큰 원판인 7이 pole3에 있기 때문에 모든 원판들은 pole3로 옮겨져야 합니다.
그러기 위해서는 6을 7 위로 옮겨야 하므로 아래와 같은 상황이 필요합니다.

여기서 6을 pole3로 옮기는 횟수 1과 (1~5)개의 원판을 pole3로 옮기는 횟수 2^5-1을 더해서 2^5을 ans변수에 더해줍니다. (ans = 32)
if (now == to) hanoi(disc - 1, to);
else
{
ans = (ans + num[disc - 1]) % MOD;
hanoi(disc - 1, sub);
}

그리고 hanoi(5, 2)를 호출하여 다시 재귀로 들어가게 되면 원판 5는 이미 pole2에 있기 때문에 hanoi(4,2)를 호출하게 됩니다. 4의 경우 pole2로 옮겨져야 하기 때문에 4를 pole2로 옮기려면 아래와 같은 상황이 필요합니다.
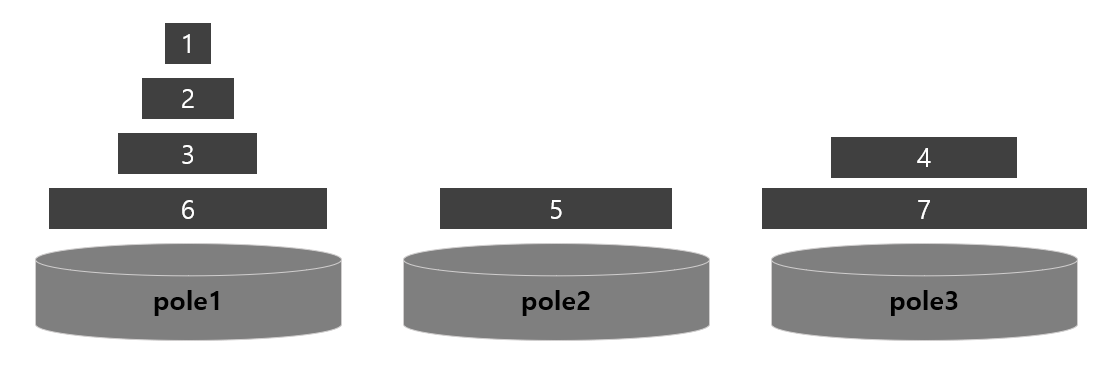
4를 pole2로 옮기는 횟수 1 과 (1~3) 원판을 pole2로 옮기는 횟수 2^3-1을 더해서 2^3을 ans변수에 더해줍니다.
(ans = 40)

그리고 hanoi(3, 1)을 호출하게 됩니다. 원판 3의 경우 pole1에 있기 때문에 hanoi(2, 1)을 호출합니다. 2가 pole1으로 옮겨지려면 1은 pole2에 있어야 하므로 2를 pole1로 옮기는 횟수 1과 1을 pole1으로 옮기는 횟수를 더해서 2를 ans 변수에 더해줍니다. (ans = 42)

따라서 답은 3번 막대기에 최소 이동 횟수 42회로 옮길 수 있습니다.
2270번: 하노이 탑
첫째 줄에 정수 n(1≤n≤100,000)이 주어진다. 둘째 줄에는 세 정수 a, b, c가 주어진다. 이는 차례로 1, 2, 3번 막대기에 꽂혀 있는 디스크의 개수이다. 이는 0이상 n이하이며, a+b+c=n이다. 다음 3개의 줄
www.acmicpc.net
풀이 참고 - ip99202.github.io/posts/%EB%B0%B1%EC%A4%80-2270-%ED%95%98%EB%85%B8%EC%9D%B4-%ED%83%91/
'🧩PS > 🥇Hard' 카테고리의 다른 글
| [C/C++] 백준 13398번 - 연속합 2 (DP) (0) | 2021.01.30 |
|---|---|
| [C/C++] 백준 10986번 - 나머지 합 (1) | 2021.01.26 |
| [C/C++] 백준 3908번 - 서로 다른 소수의 합 (0) | 2021.01.25 |
| [C/C++] 백준 9252번 - LCS 2 (Longest Common Subsequence, 최장 공통 부분 수열) (0) | 2021.01.19 |
| [C/C++] 백준 2629번 - 양팔저울 (DP풀이) (0) | 2021.01.15 |