반응형
<문제>
프로그램 명: coci_intersect
제한시간: 1 초
n 각형의 볼록 다각형이 주어질 때 대각선끼리 교차하는 점의 수를 구하는 것이 문제이다. 단, 세 개의 대각선이 한 점에서 만나는 경우는 없다.
참고로 볼록 다각형이란 내각의 크기가 180 도 미만인 다각형이다.
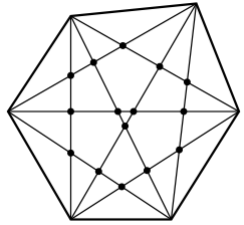
아래 그림은 6 각형의 예이다.
입력
3 이상 100 이하인 정수 n 이 입력으로 주어진다.
출력
교차점의 수를 출력한다.
입출력 예
입력 3
출력 0
입력 4
출력 1
입력 6
출력 15
<코드>
def fac(a):
if a == 1:
return 1
return a*fac(a-1)
n = int(input())
print(round(fac(n)/fac(4)/fac(n-4)))2006년도 7월 Croatian Open Competition in Informatics(COCI) contest2 4 기출문제입니다. 1시간동안 팔각형까지 그려서 규칙을 찾아내다가 이건 좀 아니다 싶어서 잘생각해보니 하나의 교차점을 이루려면 2개의 직선이 교차해야하는데 2개의 직선이 교차하려면 4개의 점이 선택되어야 합니다. 그래서 고등학교때 배웠었던 순열과 조합을 이용하여 쉽게 풀 수 있었습니다.
<순열과 조합 기본 공식>

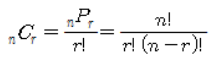
n 각형에서 4개의 점을 선택하여 서로 교차되게 그으면 각각의 교차점이 생기고 겹치지 않으므로 답은
$\combi{\ }_n\combi{C}_4$ nC4
이 됩니다.
문제 출처 - http://59.23.150.58/30stair/
step by step...30 계단
문제수: 744 30 계단 최근 게시 문제:
59.23.150.58
반응형
'🧩PS > 🥈Nomal' 카테고리의 다른 글
| [PYTHON] 층 수 구하기 (완전이진트리) (0) | 2020.02.22 |
|---|---|
| [PYTHON] 완전그래프 선의 개수 구하기 (0) | 2020.02.22 |
| [PYTHON] 45분 전 시간 구하기 (0) | 2020.02.22 |
| [PYTHON] 윤년 (0) | 2020.02.22 |
| [C/C++/PYTHON] 백준 2493번 탑(Stack, DP) (0) | 2020.02.19 |