
<코드>
#include<iostream>
#include<algorithm>
using namespace std;
int n, m, ans;
char c;
int map[1001][1001];
int dp[1001][1001];
int main()
{
ios_base::sync_with_stdio(0);
cin.tie();
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> c;
map[i][j] = c - '0';
if (i == n || j == m)
dp[i][j] = map[i][j];
ans = max(ans, dp[i][j]);
}
}
for (int i = n-1; i >= 1; i--)
{
for (int j = m - 1; j >= 1; j--)
{
if (map[i][j] != 1) continue;
if (dp[i + 1][j] == dp[i][j + 1])
{
int size = dp[i + 1][j];
if (map[i + size][j + size] == 1) dp[i][j] = size + 1;
else dp[i][j] = size;
}
else
{
dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) + 1;
}
ans = max(ans, dp[i][j]);
}
}
cout << ans * ans;
}
<dp의 정의>
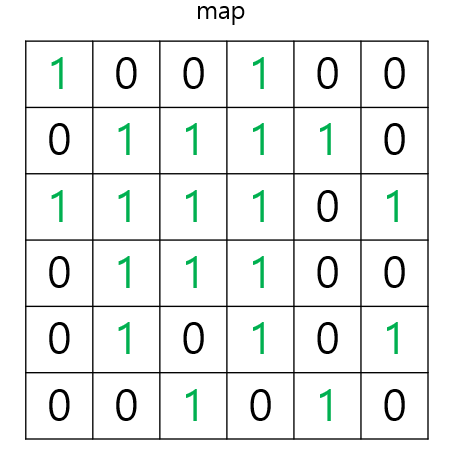
이러한 입력이 주어졌다고 가정할 때 제가 정의한 dp값의 의미는
dp[i][j] : (i, j)에서 오른쪽과 아래만으로 정사각형을 만들 때 가장 큰 정사각형 한 변의 길이
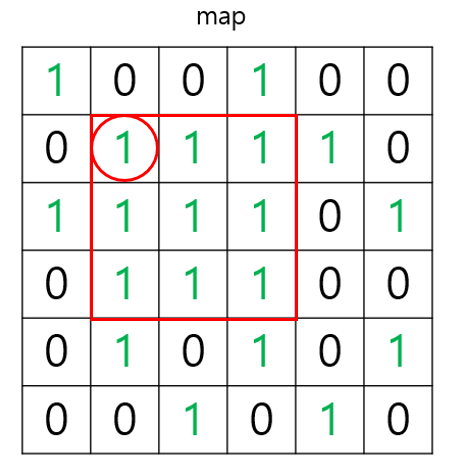
그림으로 살펴보자면 (1, 1)에서 만들 수 있는 가장 큰 정사각형 한변의 길이는 3이므로
dp[1][1] = 3입니다.
풀이 방법
1. dp배열의 맨 오른쪽과 맨 아래쪽 값들을 map배열 값으로 설정해준다. (초기값 세팅)
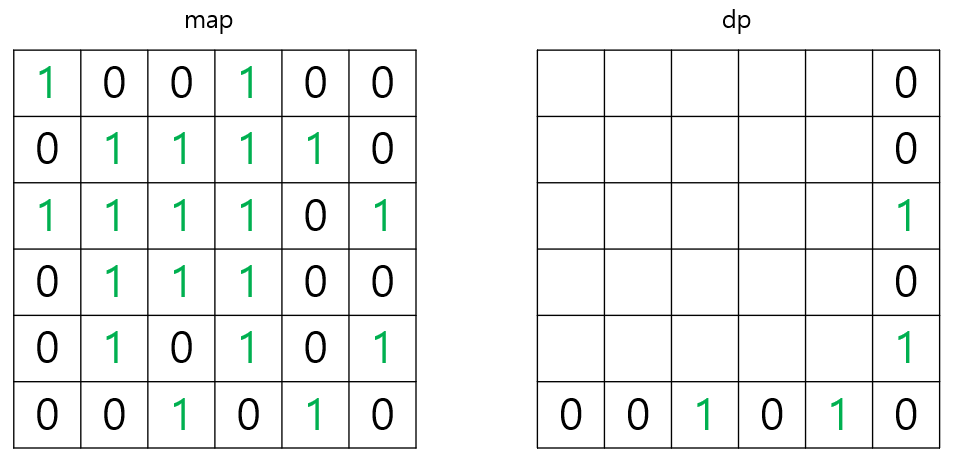
맨 오른쪽 값들과 맨 아래쪽 값들로 만들 수 있는 정사각형의 최대 크기는 1이기 때문입니다. (2 이상 만들지 못함!)
2. dp값 구하기
dp값을 구하는 과정은 (n-1, m-1)에서 (1, 1)까지 역순으로 탐색을 합니다.
for (int i = n-1; i >= 1; i--)
{
for (int j = m - 1; j >= 1; j--)
{
// dp값 구하기
}
}
따라서 dp[i][j] 값을 구할 때는 이미 dp[i+1][j], dp[i][j+1] 값이 구해져 있습니다.
예시로 아래와 같은 상황이라고 가정하면
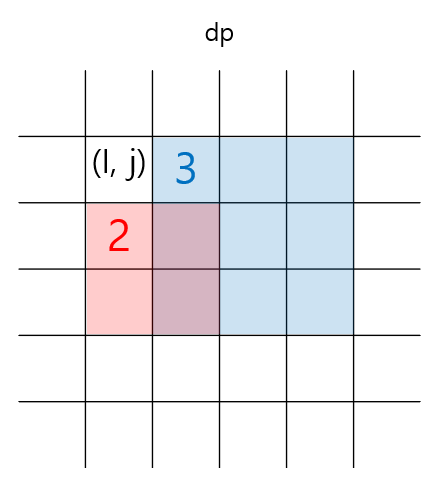
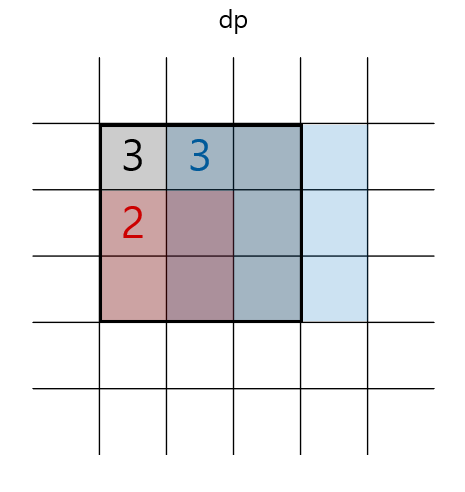
dp[i][j+1] = 3, dp[i+1][j] = 2입니다.
따라서 dp[i][j] 값은 dp[i][j+1] 과 dp[i+1][j]의 값 중에서 작은 값에다가 +1을 한 값으로 결정됩니다.
그러나 만약 dp[i+1][j] == dp[i][j+1]라면??
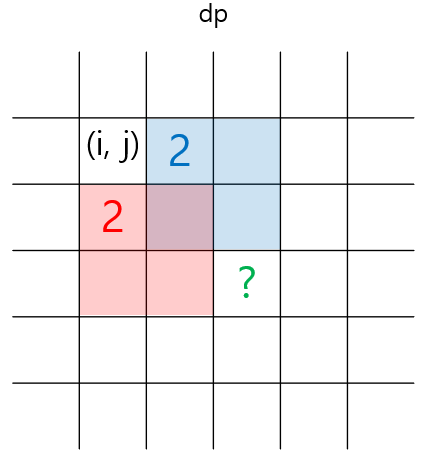
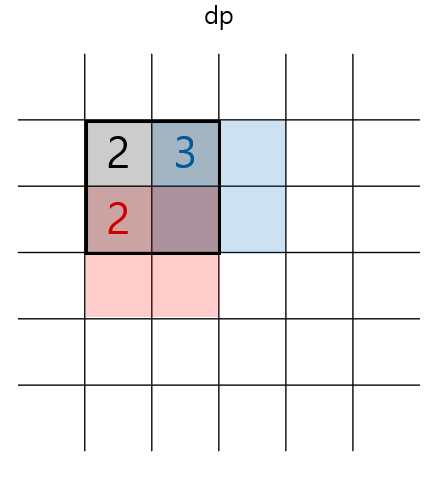
초록색의 '?' 부분의 값이 map배열에서 1인지 아닌지에 따라서 dp[i][j]의 값이 결정됩니다.
만약 map[i+2][j+2] 값이 1이라면 dp[i][j] = 3,
map[i+2][j+2] 값이 0이라면 dp[i][j] = 2로 결정됩니다.
1915번: 가장 큰 정사각형
첫째 줄에 n, m(1 ≤ n, m ≤ 1,000)이 주어진다. 다음 n개의 줄에는 m개의 숫자로 배열이 주어진다.
www.acmicpc.net
'🧩PS > 🥈Nomal' 카테고리의 다른 글
| [C/C++] 백준 2636번 - 치즈 (0) | 2021.03.26 |
|---|---|
| [C/C++] 백준 1600번 - 말이 되고픈 원숭이 (0) | 2021.03.26 |
| [C/C++] 백준 14425번 - 문자열 집합 (0) | 2021.03.25 |
| [C/C++] 백준 17404번 - RGB거리 2 (0) | 2021.03.23 |
| [C/C++] 백준 14501번 - 퇴사 (0) | 2021.03.22 |