
<코드>
#include<iostream>
#include<algorithm>
using namespace std;
int N, M, ans, sum;
int bite[101], cost[101];
int dp[101][10001];
int main()
{
cin >> N >> M;
for (int i = 1; i <= N; i++) cin >> bite[i];
for (int i = 1; i <= N; i++)
{
cin >> cost[i];
// sum : 모든 비용들의 합
sum += cost[i];
}
// dp[i][j] == i번째 앱까지 탐색했을 때
// j비용을 소모해서 얻을 수 있는 최대 메모리
for (int i = 1; i <= N; i++)
{
for (int j = 0; j <= sum; j++)
{
if (j - cost[i] >= 0)
dp[i][j] = max(dp[i][j], dp[i - 1][j - cost[i]] + bite[i]);
dp[i][j] = max(dp[i][j], dp[i - 1][j]);
}
}
for (int i = 0; i <= sum; i++)
{
if (dp[N][i] >= M)
{
cout << i << endl;
break;
}
}
}
풀이 방법
dp[i][j] : i번째 앱까지 확인했을 때 j의 비용으로 얻을 수 있는 최대의 메모리.
위의 정의대로 N번의 앱까지 모든 탐색을 끝냈을 때 dp[N][j]의 값은 j의 비용으로 얻을 수 있는 최대의 메모리 크기입니다. 즉, 사용할 수 있는 j의 비용이 늘어날수록 얻을 수 있는 메모리도 늘어날 텐데 처음으로 M을 넘는 j값이 바로 이 문제의 정답이 됩니다.
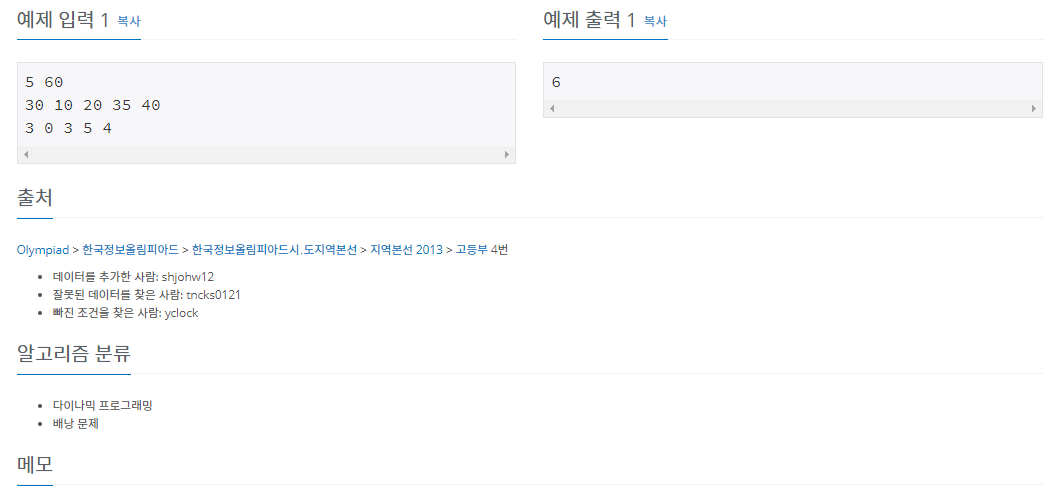
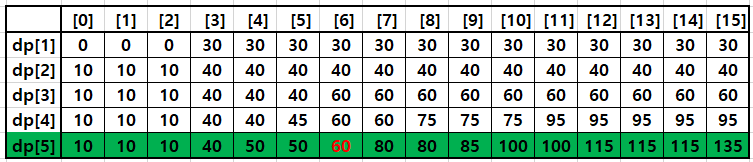
예제 입력 1이 입력으로 주어질 때 dp배열 값을 살펴보겠습니다.

// dp[i][j] == i번째 앱까지 탐색했을 때
// j비용을 소모해서 얻을 수 있는 최대 메모리
for (int i = 1; i <= N; i++)
{
for (int j = 0; j <= sum; j++)
{
if (j - cost[i] >= 0)
dp[i][j] = max(dp[i][j], dp[i - 1][j - cost[i]] + bite[i]);
dp[i][j] = max(dp[i][j], dp[i - 1][j]);
}
}입력에서 5개의 앱들의 비활성화 비용의 합 sum은 15입니다. 따라서 dp배열도 j=15번까지만 출력을 하였습니다. 비용의 경우 최악의 경우 최대 100*100 이므로 dp[100][10000] 배열을 선언하더라고 메모리 초과가 발생하지 않습니다.
i가 1일 때 dp[1][0]은 0입니다. 왜냐하면 1번 앱의 비용은 3인데 0의 비용으로는 1번 앱을 비 활성시켜서 메모리를 확보할 수 없기 때문입니다. 1번 앱을 종료시키기 위해서는 비용이 적어도 3이 필요하기 때문에 dp[1][3]부터 dp[1][15]까지의 값은 30입니다.
i가 2일 때 2번 앱의 비활성 비용은 0이므로 모든 dp값을 +10 해줍니다.
이런 식으로 계속 dp값을 구해주고 dp[3][6]을 살펴보겠습니다.
dp[i-1][j-cost[i]]인 dp[2][3] = 40은 2번 앱까지 살펴봤을 때 3의 비용을 사용해서 얻을 수 있는 최대 메모리는 40이라는 의미를 가지고 있습니다. dp[3][6]도 마찬가지로 3번 앱까지 살펴보고 6의 비활성 비용을 소모할 때 얻을 수 있는 최대 메모리 크기라는 의미를 가지고 있으며, 3번 앱의 비활성 비용이 3이고 메모리 크기가 20이므로 dp[3][6]에는 60이 저장되게 됩니다.
그리하여 dp[N]의 원소들 중에서 처음으로 M이상인 j(비용) 값이 이 문제의 정답이 됩니다.
7579번: 앱
입력은 3줄로 이루어져 있다. 첫 줄에는 정수 N과 M이 공백문자로 구분되어 주어지며, 둘째 줄과 셋째 줄에는 각각 N개의 정수가 공백문자로 구분되어 주어진다. 둘째 줄의 N개의 정수는 현재 활
www.acmicpc.net
'🧩PS > 🥇Hard' 카테고리의 다른 글
| [C/C++] 백준 17298번 - 오큰수 (스택) (7) | 2021.01.06 |
|---|---|
| [C/C++] 백준 11438번 - LCA2 (Lowest Common Ancestor, 최소 공통 조상) (0) | 2020.12.28 |
| [C/C++] 백준 11049번 - 행렬 곱셈 순서 (DP) (5) | 2020.12.26 |
| [C/C++] 백준 11066번 - 파일 합치기 (DP) (1) | 2020.12.26 |
| [C/C++] 백준 1725번 - 히스토그램 (스택 풀이) (3) | 2020.12.25 |