

<코드>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
int N, M;
int u, v;
queue<int> q;
vector<int> node[100001];
bool check[100001];
int parent[100001][20];
int depth[100001];
int LCA(int u, int v)
{
// v가 u보다 더 깊은 노드로 세팅
if (depth[u] > depth[v]) swap(u, v);
// 두 노드의 깊이가 같아질때까지 v노드는 위로 거슬러 올라감
while (depth[u] != depth[v])
{
// 두 노드의 깊이 차이
int dist = depth[v] - depth[u];
for (int i = 0; i < 20; i++)
{
if (dist <= (2 << i))
{
// 2^i 만큼 거슬러 오라감
v = parent[v][i];
break;
}
}
}
// 두 노드가 같아질때 까지 위로 거슬러 올라감
while (u != v)
{
for (int i = 0; i < 20; i++)
{
if (parent[u][i + 1] == parent[v][i + 1])
{
u = parent[u][i];
v = parent[v][i];
break;
}
}
}
return u; // LCA 리턴
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> N;
// 해당노드에 연결된 노드 push
for (int i = 0; i < N - 1; i++)
{
cin >> u >> v;
node[u].push_back(v);
node[v].push_back(u);
}
check[1] = true;
q.push(1); // 트리의 루트
while (!q.empty())
{
int x = q.front(); // 부모 노드
q.pop();
for (int i = 0; i < node[x].size(); i++)
{
int child = node[x][i];
if (!check[child]) // 현재노드를 방문한적 없다면
{
depth[child] = depth[x] + 1; // 깊이 +1
check[child] = true; // 방문표시
parent[child][0] = x;
for (int j = 0; j < 20; j++) // 부모노드 입력
{
// 현재노드에서 2^(j+1) 위에 있는 부모 노드는
// 2^j 위에 있는 부모노드의 2^j 위에 있는 부모노드
parent[child][j + 1] = parent[parent[child][j]][j];
// 2^(j+1) 위에 부모노드가 없을 경우
if (parent[child][j + 1] == 0) break;
}
q.push(child); // 큐에 추가
}
}
}
cin >> M;
for (int i = 0; i < M; i++)
{
cin >> u >> v;
cout << LCA(u, v) << '\n';
}
}
비슷한 문제
[C/C++] 백준 11437번 - LCA (Lowest Common Ancestor, 최소 공통 조상)
<코드> #include #include #include #include using namespace std; int N, M; int u, v; queue q; vector node[50001]; bool check[50001]; int parent[50001]; int depth[50001]; int LCA(int u, int v) { //..
cocoon1787.tistory.com
풀이 방법

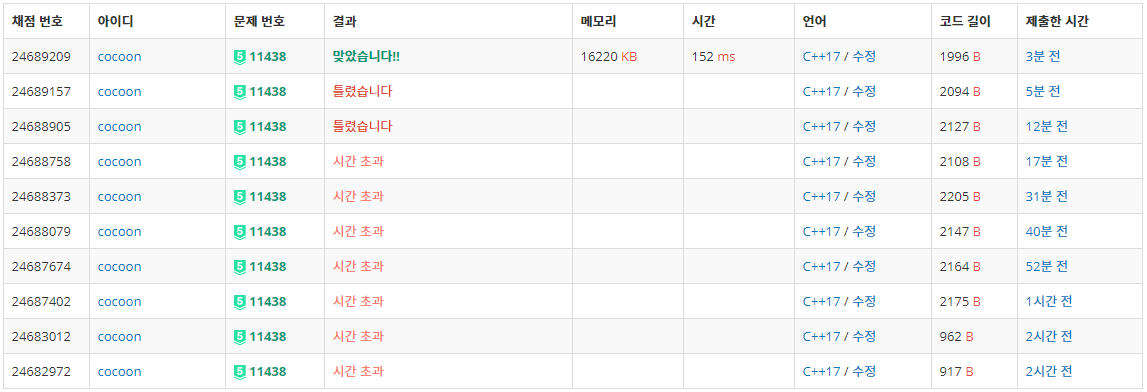
백준 11437번 LCA 문제에서는 정점의 개수가 5만 개, 질문의 개수가 1만 개였지만, 이번 문제(11438번 LCA2)는 정점의 개수와 질문의 개수가 모드 10만이므로 11437번의 코드는 시간 초과가 발생하게 됩니다. 따라서 원래 1차원이었던 parent배열을 2차원으로 선언하여 2^j 위에 있는 부모의 노드를 기록하도록 하였습니다.
parent[i][j] : i 노드의 2^j 위에 있는 부모의 노드.
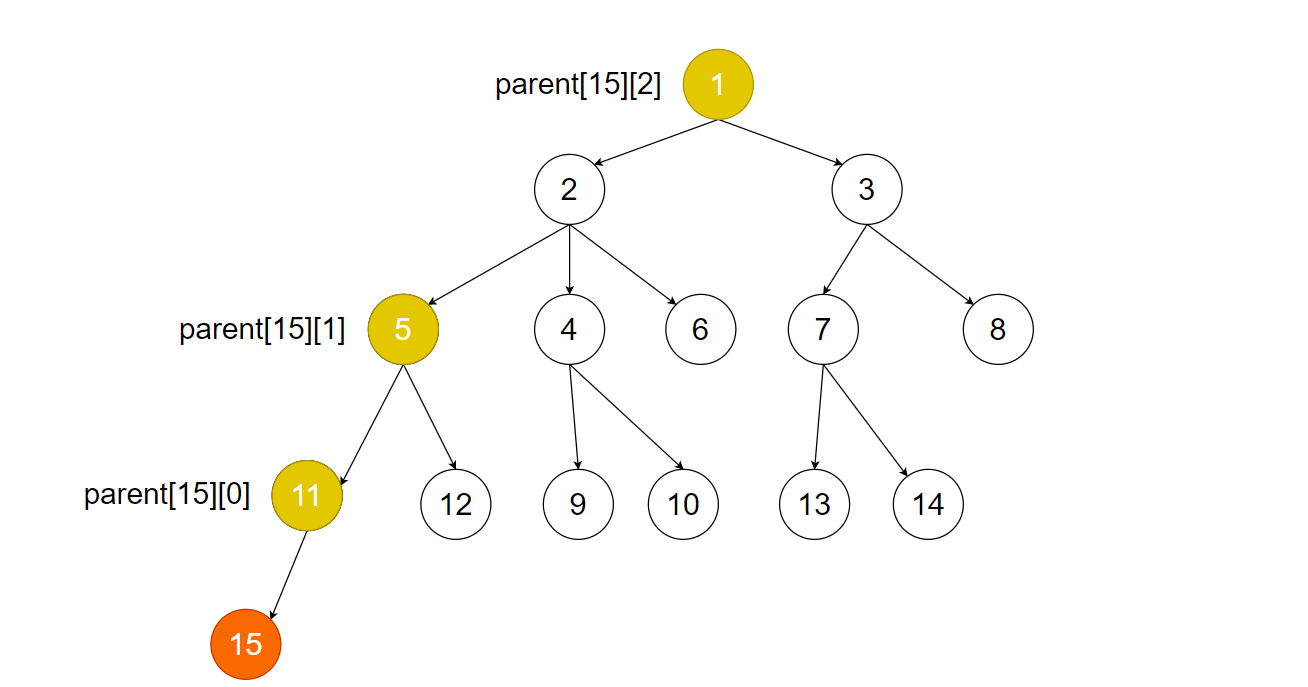
위의 그림에서 보이듯이
15번 노드의 2^0 위에 있는 부모 노드는 11입니다.
15번 노드의 2^1 위에 있는 부모 노드는 5입니다.
15번 노드의 2^2 위에 있는 부모 노드는 1입니다.
Q : 왜 이런 식으로 저장을 해야 하나요?

A : 최악의 경우 정점의 개수가 10만 개이므로 한 칸씩 위로 거슬러 올라가면서 부모 노드를 찾는 알고리즘은 시간 초과가 발생하게 됩니다. 따라서 2차원 배열 parent 배열을 통해 2^j 위에 있는 부모의 노드를 알고 있을 경우 O(N)이 아닌 O(logN)만에 부모 노드를 찾을 수 있게 됩니다.
<코드 설명>
while (!q.empty())
{
int x = q.front(); // 부모 노드
q.pop();
for (int i = 0; i < node[x].size(); i++)
{
int child = node[x][i];
if (!check[child]) // 현재노드를 방문한적 없다면
{
depth[child] = depth[x] + 1; // 깊이 +1
check[child] = true; // 방문표시
parent[child][0] = x;
for (int j = 0; j < 20; j++) // 부모노드 입력
{
// 현재노드에서 2^(j+1) 위에 있는 부모 노드는
// 2^j 위에 있는 부모노드의 2^j 위에 있는 부모노드
parent[child][j + 1] = parent[parent[child][j]][j];
// 2^(j+1) 위에 부모노드가 없을 경우
if (parent[child][j + 1] == 0) break;
}
q.push(child); // 큐에 추가
}
}
}
먼저 BFS를 통해서 모든 노드를 방문할 것이고 각각의 노드를 방문할 때 부모 노드를 저장하고 노드의 깊이 또한 저장합니다.
parent[child][j + 1] = parent[parent[child][j]][j];위 코드의 예시를 들자면 parent[11][3]는 11번 노드의 2^3 위에 있는 부모 노드입니다. 즉, 11번 노드의 2^2 위에 있는 노드의 2^2 위에 있는 노드라는 말입니다. 아래의 그림에서 parent[11][3]은 11번 노드보다 8만큼 위에 있는 Y 노드입니다. Y노드는 X노드에서 4만큼 위에 있는 부모 노드이기도 합니다.
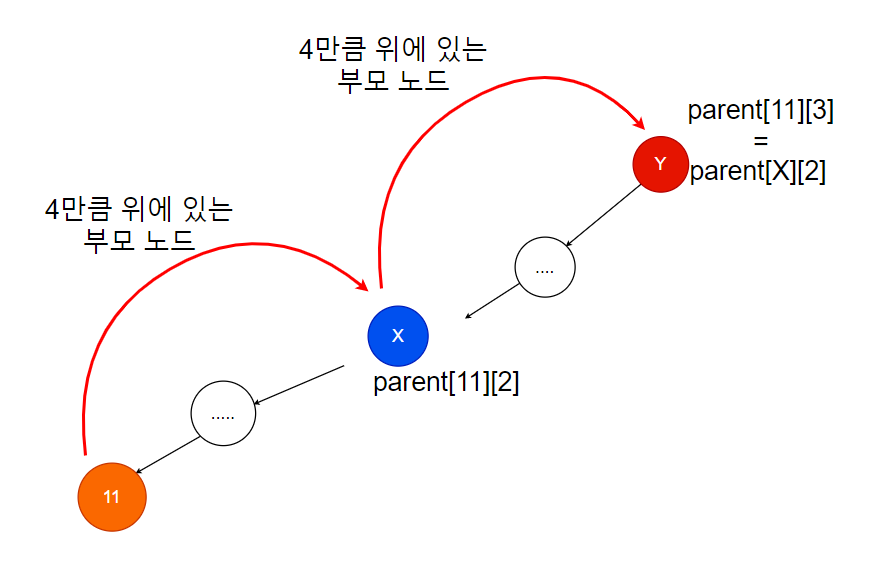
따라서
parent[11][3] = parent[parent[11][2]][2] 입니다.
int LCA(int u, int v)
{
// v가 u보다 더 깊은 노드로 세팅
if (depth[u] > depth[v]) swap(u, v);
// 두 노드의 깊이가 같아질때까지 v노드는 위로 거슬러 올라감
while (depth[u] != depth[v])
{
// 두 노드의 깊이 차이
int dist = depth[v] - depth[u];
for (int i = 0; i < 20; i++)
{
if (dist <= (2 << i))
{
// 2^i 만큼 거슬러 오라감
v = parent[v][i];
break;
}
}
}
// 두 노드가 같아질때 까지 위로 거슬러 올라감
while (u != v)
{
for (int i = 0; i < 20; i++)
{
if (parent[u][i + 1] == parent[v][i + 1])
{
u = parent[u][i];
v = parent[v][i];
break;
}
}
}
return u; // LCA 리턴
}LCA를 구하는 코드에서는 두 노드의 깊이를 맞춰준 다음 두 노드의 부모 노드가 같아질 때까지 2의 x승씩 올라가면서 찾게 됩니다.
만약 깊이 8에서 1로 올라가는 상황을 생각해보면 한 칸씩 거슬러 올라갈 경우 7번의 연산을 해야 하지만 2의 x승씩 올라가게 된다면 4+2+1로 3번의 연산만으로 올라갈 수 있습니다.
<parent 2차원 배열의 모습>
<출력 코드>
for (int i = 0; i < 20; i++)
{
for (int j = 0; j < 20; j++)
{
printf("%2d", parent[i][j]);
}
cout << endl;
}

parent[2][0] 과 parent[3][0]은 각각 2와 3의 2^0 위에 있는 부모이므로 둘 다 "1"번 노드입니다.
parent[4][0], parent[5][0], parent[6][0]의 경우 2^0 위에 있는 부모는 모두 "2"번 노드입니다.
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
'🧩PS > 🥇Hard' 카테고리의 다른 글
| [C/C++] 백준 11444번 - 피보나치 수 6 (점화식, 분할 정복) (5) | 2021.01.06 |
|---|---|
| [C/C++] 백준 17298번 - 오큰수 (스택) (7) | 2021.01.06 |
| [C/C++] 백준 7579번 - 앱 (DP) (2) | 2020.12.26 |
| [C/C++] 백준 11049번 - 행렬 곱셈 순서 (DP) (5) | 2020.12.26 |
| [C/C++] 백준 11066번 - 파일 합치기 (DP) (1) | 2020.12.26 |