문제
방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.
입력
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10 이하의 자연수이다. 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.
출력
첫째 줄부터 V개의 줄에 걸쳐, i번째 줄에 시작점에서 i번 정점까지의 최단 경로의 경로값을 출력한다. 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력하면 된다.

<코드>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
#define INF 1000000000 // 10억
int V, E, K;
int u, v, w;
int weight, node, next_weight, next_node;
int ans[20001];
vector<pair<int, int>> vec[20001];
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
int main()
{
cin >> V >> E >> K;
for (int i = 1; i <= V; i++) ans[i] = INF;
for (int i = 0; i < E; i++)
{
cin >> u >> v >> w;
vec[u].push_back(pair<int, int>(v, w));
}
ans[K] = 0;
pq.push(make_pair(0, K)); // 가중치 크기순서대로 넣기위해 (가중치,노드)으로 push
while (!pq.empty())
{
weight = pq.top().first;
node = pq.top().second;
pq.pop();
for (int i = 0; i < vec[node].size(); i++)
{
next_node = vec[node][i].first;
next_weight = weight + vec[node][i].second;
if (ans[next_node] > next_weight)
{
ans[next_node] = next_weight;
pq.push(make_pair(next_weight, next_node));
}
}
}
for (int i = 1; i <= V; i++)
{
if (ans[i] == INF) cout << "INF" << '\n';
else cout << ans[i] << '\n';
}
}
풀이 방법
다익스트라란?
다익스트라는 음의 가중치가 없는 그래프의 한 정점에서 모든 정점까지의 최단거리를 구하는 알고리즘이다. 다익스트라의 기본 로직은 먼저 모든 정점들을 무한대 값으로 설정한 뒤 시작 정점을 기준으로 연결되어있는 정점들을 연결하며 최단 거리를 갱신하는 것이다.
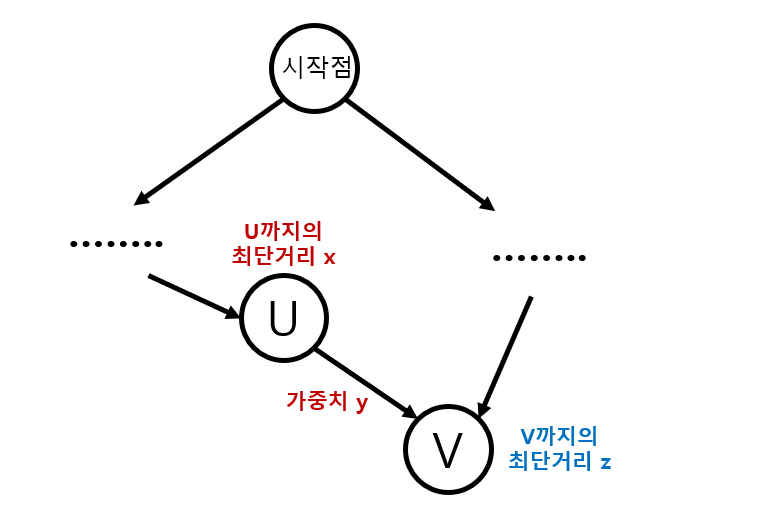
예를 들어 정점 U에서 V로 이어지게 된다면,
시작점~정점 U까지의 최단거리+U~V 간선의 가중치 와 기존의 V까지의 최단거리 를 비교하여 시작점에서 V까지의 최단 거리를 갱신한다.
위의 문제를 풀 때 모든 정점과 간선의 정보를 저장하기 위해 단순히 int형으로 인접 행렬을 생성할 시 20000*20000*4byte = 1,600,000,000byte = 1600MB로 메모리 초과가 발생하게 된다.
따라서 인접 리스트를 활용하여 정점과 간선의 연결 정보를 저장하는데

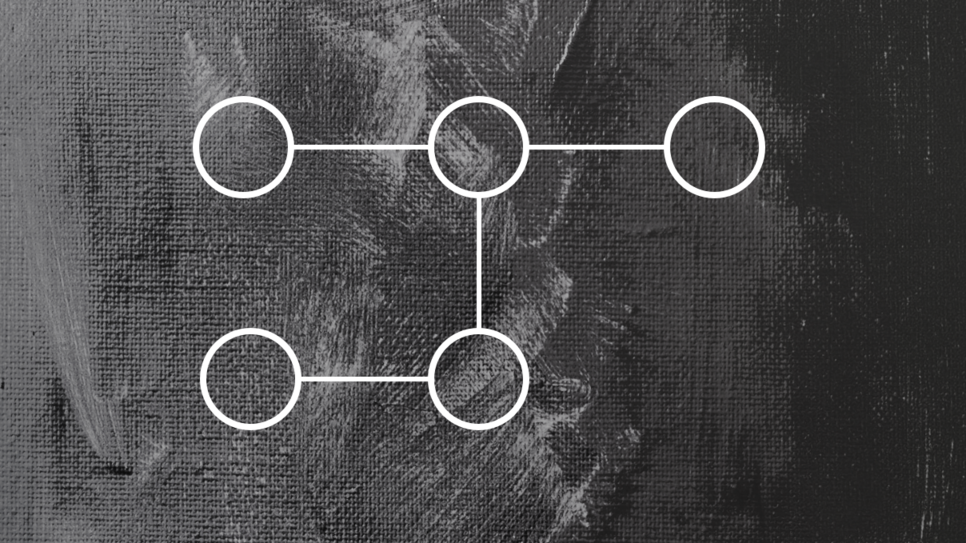
예제 입력 1의 그래프를 인접 리스트로 저장한다면 다음과 같다.
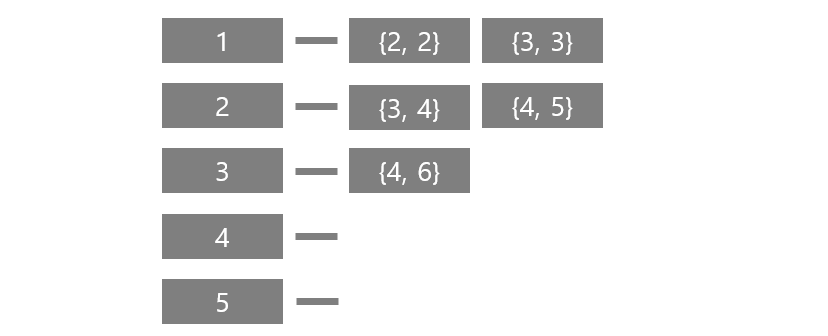

각각의 리스트들은 {정점, 가중치} 정보를 담고 있으며, 예를 들어 2번 정점의 경우 {3, 4}, {4, 5}를 담고 있으므로
{3, 4} -> 3번과 가중치 4로 연결되어있음.
{4, 5} -> 4번과 가중치 5로 연결되어있음.
vector<pair<int, int>> vec[20001];코드에서 벡터 vec은 인접 리스트의 역할을 한다.
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;그리고 제한시간 타이트하기 때문에 우선순위 큐를 사용하였고 우선순위 큐의 정렬 defalut값은 내림차순이기 때문에 위와 같이 오름차순으로 우선순위 큐를 선언하였다.
< 자세한 설명 (예제 입력 1을 예시로) >


| 1 | 2 | 3 | 4 | 5 |
| 0 | INF | INF | INF | INF |
1. pq에 초기값으로 (0, 1)를 push 한다. node = 1, weight = 0으로 저장되고 pq를 pop 한다.
2. vec[node] == vec[1]에는 {2, 2}와 {3, 3}이 들어있다. 2번과 3번 정점 모두 INF이므로 최단거리를 갱신해주고 pq에 {2,2}, {3,3}을 push 해준다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | INF | INF | INF | INF |
| 2 | 3 |
| pq | {2, 2}, {3, 3} | |||
3. pq의 top은 {2, 2}이므로 node = 2, weight = 2가 되며 pq를 pq를 pop 해준다.
vec[2]에는 {3,4}, {4,5}가 있므로 먼저 {3, 4}에서
(2번 정점 최단거리 = 2) + (2~3번 간선 가중치 = 4) = 6
3번 정점 최단거리 = 3 이므로 최단거리를 갱신하지 않고, 다음 {4, 5}에서는
(2번 정점 최단거리 = 2) + (2~4번 간선 가중치 = 5) = 7
4번 정점 최단거리 = INF 이므로 최단거리를 갱신해준다. 그리고 {7,4}를 pq에 push 한다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | INF | INF | INF | INF |
| 2 | 3 | 7 |
| pq | {3, 3}, {7, 4} | |||
4. pq의 top은 {3, 3}이므로 node = 3, weight = 3가 되며 pq를 pq를 pop 해준다.
vec[3]에는 {4, 6}가 있으므로
(3번 정점 최단거리 = 3) + (3~4번 간선 가중치 = 6) = 9
4번 정점 최단거리 = 7 이므로 최단거리를 갱신하지 않는다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | INF | INF | INF | INF |
| 2 | 3 | 7 |
| pq | {7, 4} | |||
5. pq의 top은 {7, 4}이므로 node = 4, weight = 7이 되며 pq를 pq를 pop 해준다.
vec[4]에는 원소가 없으므로 for문에 진입하지 못하고 pq가 비어있으므로 while문이 종료된다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | INF | INF | INF | INF |
| 2 | 3 | 7 |
| pq | ||||
따라서 답은 "0 2 3 7 INF"가 된다.
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다.
www.acmicpc.net
'🧩PS > 🥇Hard' 카테고리의 다른 글
| [C/C++] 백준 2629번 - 양팔저울 (DP풀이) (0) | 2021.01.15 |
|---|---|
| [C/C++] 백준 1450번 - 냅색문제 (0) | 2021.01.10 |
| [C/C++] 백준 11444번 - 피보나치 수 6 (점화식, 분할 정복) (5) | 2021.01.06 |
| [C/C++] 백준 17298번 - 오큰수 (스택) (7) | 2021.01.06 |
| [C/C++] 백준 11438번 - LCA2 (Lowest Common Ancestor, 최소 공통 조상) (0) | 2020.12.28 |