
<코드>
#include<iostream>
#include<algorithm>
using namespace std;
int N, K;
int a, b;
int seg[(1<<18)];
// 세그먼트트리 초기화
int init(int node, int s, int e) // (루트노드, 시작, 끝)
{
if (s == e) return seg[node] = 1; // start 와 end 의 위치가 일치하면 1을 넣어준다.
int mid = (s + e) / 2;
return seg[node] = init(2 * node, s, mid) + init(2 * node + 1, mid + 1, e);
}
// 세그먼트트리 정보 수정
int update(int node, int s, int e, int del) // (루트노드, 시작, 끝, 제거번호)
{
seg[node]--;
if (s == e) return 0;
else
{
int mid = (s + e) / 2;
if (del <= mid) return update(2 * node, s, mid, del);
else return update(2 * node + 1, mid + 1, e, del);
}
}
// 다음 순서에 해당하는 번호 받아오기
int query(int node, int s, int e, int order) // (현재노드, 시작, 끝, 순서)
{
if (s == e) return s; // start 와 end 의 위치가 일치하면 번호를 반환한다.
int mid = (s + e) / 2;
if (order <= seg[2 * node]) return query(2 * node, s, mid, order);
else return query(2 * node + 1, mid + 1, e, order - seg[2 * node]);
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie();
cin >> N >> K;
init(1, 1, N); // (루트노드, 시작, 끝)
int index = 1;
cout << "<";
for (int i = 0; i < N; i++)
{
// 다음 순서 구하기
int size = N - i; // 사람 수
index += K - 1;
if (index % size == 0) index = size;
else if (index > size) index %= size;
// 다음 순서에 해당하는 번호 받아오기
int num = query(1, 1, N, index);
// 해당 번호 제거 하기
update(1, 1, N, num);
if (i == N - 1) cout << num;
else cout << num << ", ";
}
cout << ">";
}
[C/C++] 백준 1158번 - 요세푸스 문제
<코드> #include #include #include using namespace std; int N, K; deque dq; int main(void) { ios_base::sync_with_stdio(0); cin.tie(); cin >> N >> K; for (int i = 1; i <= N; i++) dq.push_back(i); cou..
cocoon1787.tistory.com
바로 위의 백준 1158번 문제는 (1 ≤ K ≤ N ≤ 5,000) 일 때의 요세푸스 문제이다. 단순하게 vector 혹은 deque 라이브러리의 erase 함수를 사용하면 간단하게 풀리는 문제이다.
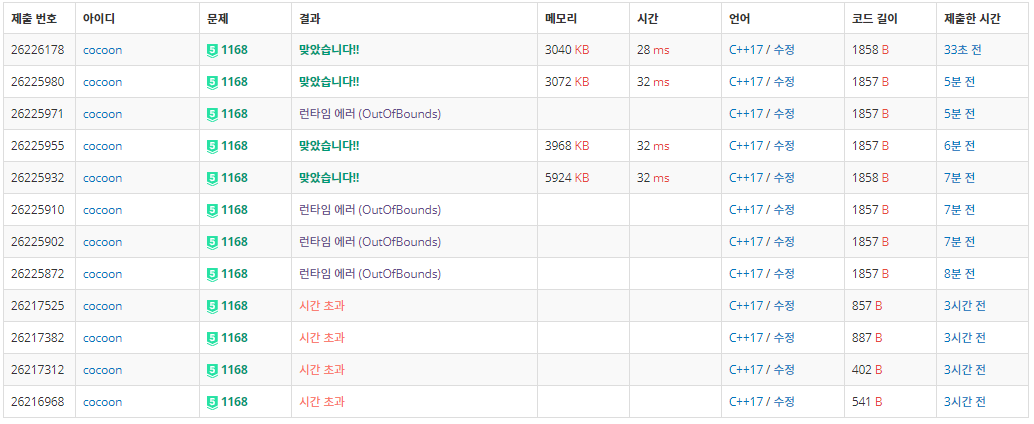
그러나 이번 백준 1168번 요세푸스 문제2는 (1 ≤ K ≤ N ≤ 100,000) 이므로 erase함수를 사용한 시간 복잡도 O(N²)의 풀이는 시간초과가 발생하게 된다. (최근에 문제가 재채점 되어 O(N²)의 풀이는 모두 오답처리 되었음)
이번 문제는 세그먼트 트리를 이용하여 O(NlogM)의 시간 복잡도로 코드를 통과시킬 수 있다.
cocoon1787.tistory.com/313 (세그먼트 트리에 관한 내용 링크)
[자료구조] 세그먼트 트리(구간트리, Segment Tree)로 구간 내 최소값 찾기
세그먼트 트리(Segment Tree)란? 알고리즘 문제를 풀다 보면 정렬되어 있지 않은 구간 내의 합이나 최솟값들을 빠르게 찾아야 하는 경우가 많습니다. 질문이 1개일 경우 간단하게 for문을 통해서 O(N)
cocoon1787.tistory.com
풀이 방법
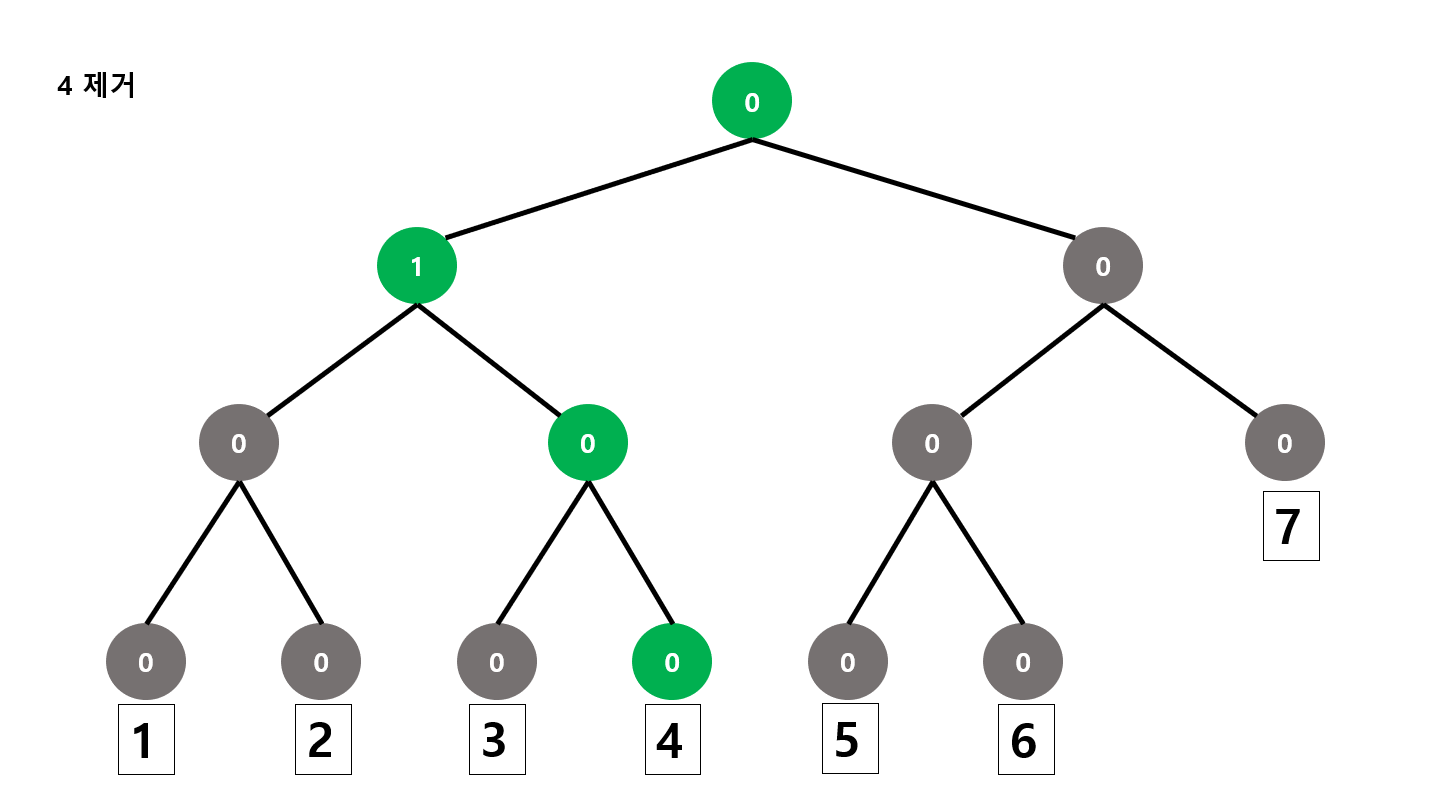
세그먼트 트리를 만드는데 N의 개수만큼 리프들을 생성하고 모든 리프들은 1로 설정한다.
모든 부모 노드는 자식 노드들의 합이다. 예제 입력 1인 "7 3"을 입력하면 아래와 같은 세그먼트 트리가 생성된다.
// 세그먼트트리 초기화
int init(int node, int s, int e) // (루트노드, 시작, 끝)
{
if (s == e) return seg[node] = 1; // start 와 end 의 위치가 일치하면 1을 넣어준다.
int mid = (s + e) / 2;
return seg[node] = init(2 * node, s, mid) + init(2 * node + 1, mid + 1, e);
}

세그먼트 트리를 생성했다면 시간 복잡도 logM만에 해당 순서의 번호를 알아낼 수 있는데
// 다음 순서에 해당하는 번호 받아오기
int query(int node, int s, int e, int order) // (현재노드, 시작, 끝, 순서)
{
if (s == e) return s; // start 와 end 의 위치가 일치하면 번호를 반환한다.
int mid = (s + e) / 2;
if (order <= seg[2 * node]) return query(2 * node, s, mid, order);
else return query(2 * node + 1, mid + 1, e, order - seg[2 * node]);
}
query함수로 order번째 번호를 알아내고
// 세그먼트트리 정보 수정
int update(int node, int s, int e, int del) // (루트노드, 시작, 끝, 제거번호)
{
seg[node]--;
if (s == e) return 0;
else
{
int mid = (s + e) / 2;
if (del <= mid) return update(2 * node, s, mid, del);
else return update(2 * node + 1, mid + 1, e, del);
}
}update함수로 del번호에 해당하는 리프를 0으로 바꿔준다.
(리프 노드로 이동하면서 해당 노드 값을 -1 해주면 자동적으로 세그먼트 트리들의 정보가 업데이트된다.)
예제 입력 1의 경우 순서는 모듈러 연산으로 구할 수 있다. (3 5 2 4 3 1 1)
{1,2,3,4,5,6,7} 7개의 수들 중 3번째 수인 3을 제거

{1,2,4,5,6,7} 6개의 수들 중 5번째 수인 6을 제거

{1,2,4,5,7} 5개의 수들 중 2번째 수인 2를 제거

{1,4,5,7} 4개의 수들 중 4번째 수인 7을 제거

{1,4,5} 3개의 수들 중 3번째 수인 5를 제거

{1,4} 2개의 수들 중 1번째 수인 1을 제거

{4} 1개의 수들 중 1번째 수인 4를 제거
1168번: 요세푸스 문제 2
첫째 줄에 N과 K가 빈 칸을 사이에 두고 순서대로 주어진다. (1 ≤ K ≤ N ≤ 100,000)
www.acmicpc.net
'🧩PS > 🥇Hard' 카테고리의 다른 글
| [프로그래머스] - 베스트앨범 (해시) (0) | 2021.03.03 |
|---|---|
| [C/C++] 백준 10217번 - KCM Travel (다익스트라) (0) | 2021.02.20 |
| [C/C++] 백준 17135번 - 캐슬 디펜스 (0) | 2021.02.08 |
| [C/C++] 백준 10159번 - 저울 (플루이드 와샬) (0) | 2021.02.08 |
| [C/C++] 백준 14938번 - 서강그라운드 (플로이드 와샬, 다익스트라) (0) | 2021.02.08 |